тогда
dqT
cT
= -LJ- ^
да.
T
dTT
В случае изотермического
подвода тепла теплоемкость стремится
к бесконечности.
Уравнение Роберта
Майера
Разность изобарной
и изохорной теплоемкостей равна удельной
газовой постоянной:
ср
- cV
= R
- уравнение Роберта Майера.
Теплоемкость газа
зависит от физических свойств газа и
его атомности (одноатомные, двухатомные,
трехатомные).
Для одноатомных
газов:
35
cv
= 2
R; cp = 5
r.
Для двухатомных
газов:
7
cv = 2 R;
cp = 2
R.
Для трехатомных
газов:
=
6 D. = 8 TJ
cv
=
2
R;
cp
=
2
Теплоемкость
идеального
газа является величиной постоянной и
не зависит от температуры. Теплоемкость
реального
газа зависит от температуры и от
атомности.
Фундаментальным
законом природы, имеющим
всеобщий характер, является закон
сохранения и превращения энергии -
энергия не исчезает и не возникает
вновь, она лишь переходит из одного
вида в другой в различных физических
и химических процессах. Закон сохранения
и превращения энергии устанавливает
однозначную связь между всеми видами
энергии в процессе их взаимопревращений.
В теплотехнике этот закон называют
первым законом термодинамики, т.е.
первый закон термодинамики имеет
всеобщий характер.
Формулировки первого
закона термодинамики:
Вечный двигатель
первого рода невозможен, т.е. невозможно
создать постоянно действующую машину,
совершающую работу без подвода энергии
извне.
В замкнутой
термодинамической системе сумма всех
видов энергии - величина постоянная.
В замкнутой
термодинамической системе алгебраическая
сумма изменений энергии равна 0.
Первый закон термодинамики
Рассмотрим следующую
систему (рис. 2.8).
К рабочему телу
(газу), находящемуся в камере, образованной
цилиндром и поршнем, от какого-либо
источника подводится элементарная
теплота dq.
Внутренняя
энергия тела u
увеличивается на малое значение du,
газ перемещает поршень на расстояние
dS,
совершая элементарную работу dl.
Рис. 2.8. Преобразование
энергии в замкнутой термодинамической
системе
Будем считать:
du
положительным (+), если внутренняя
энергия в процессе увеличивается,
отрицательным (-), если внутренняя
энергия уменьшается;
dl
положительным (+), если работа совершается
рабочим телом (работа расширения),
отрицательным (-), если работа совершается
над рабочим телом (например, какая-либо
внешняя сила с помощью поршня сжимает
рабочее тело, совершая работу сжатия).
dq
положительным (+), если теплота подводится
к тепловому источнику от рабочего
тела, отрицательным (-), если теплота
отводится от теплового источника и
подводится к рабочему телу.
Рассматриваемая
система полностью изолирована от
окружающей среды, поэтому можно записать
следующее уравнение:
-dq
+ du
+ dl
= 0, или dq
= du
+ dl.
В общем случае тепло
подводимое к рабочему телу идет на
изменение его внутренней энергии и
совершение работы.
Работа газа
Вычислим работу
рабочего тела в зависимости от изменения
объема на примере расширения газа в
цилиндре под поршнем.
На рис 2.9 показан
цилиндр с перемещающимся под давлением
газа поршнем и соответствующая данному
термодинамическому процессу диаграмма
состояния рабочего тела в координатах
р
- v.
F
- площадь поршня.
В точке 1 (начало
термодинамического процесса) газ
занимает объем v1,
в точке 2
(конец термодинамического процесса)
газ занимает объем v2.
Рассмотрим малое
перемещение поршня dx
(которому соответствует изменение
объема dv), при котором
совершается элементарная работа dl.
В данном случае
сила, с которой газ действует на поршень,
равна произведению давления газа
на площадь днища поршня:
A =
pF.
В процессе 1 - 2
давление газа изменяется, однако на
участке элементарного перемещения
dx
значение давления можно считать
постоянным: р
= const.
Поскольку работа
газа - это произведение приложенной
силы на расстояние, то
dl
= Adx
= pFdx.
Изменение объема:
dv
= Fdx.
Окончательно
получим:
dl
= pdv.
Тогда работа
рассматриваемой системы при переходе
из состояния 1 в 2 определяется:
l
1-2
где p
= f(v).
Геометрическое
истолкование работы газа
В системе координат
P
- v
площадь под линией процесса численно
равна работе. Рассмотрим некоторые
примеры.
На рис. 2.10, а
изображен процесс перехода состояния
рабочего тела (газа) из точки 1 в точку
2. Стрелкой показано направление
процесса. Газ расширяется и совершает
работу, объем газа увеличивается, а
давление снижается.
На рис. 2.10, б
процесс идет от точки 2 к точке 1. В данном
случае работа отрицательная, т.е.
совершается внешними силами над газом.
На рис. 2.10, в
показан изохорный процесс, при котором
объем рабочего тела постоянный, а
площадь под линией 1 - 2 и работа равны
0.
P
P
P
4
1
2'
А
~t2
ll-2
= 0
1''
v
в
Рис.
2.10. Термодинамические процессы: а
- работа процесса положительная;
б - работа процесса отрицательная;
в - работа процесса
= 0
Также отметим, что
величина работы зависит не только от
начальных параметров, но и от процессов
перехода из одного состояния в другое.
На рис. 2.11 показаны
термодинамические процессы перехода
тела из точки 1 в точку 2. Очевидно, что
площадь (а значит, и работа газа) под
линией процесса а
больше, чем площадь под линией b.
Р
Рис. 2.11.
Термодинамические процессы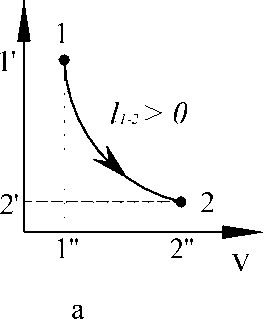
Теплота
Теплота является
одним из наиболее важных понятий
термодинамики. По своему существу
понятие теплоты близко к понятию работы.
Теплота и работа являются формами
передачи энергии. Поэтому нет смысла
говорить, что тело обладает каким-то
запасом теплоты или работы. Можно лишь
констатировать, что телу сообщена (или
от тела отнята) определенная теплота
или определенная работа.
Различие между
теплотой и работой состоит в том, что
они являются различными формами
передачи энергии. Теплота представляет
собой такую форму передачи энергии,
которая определяется либо непосредственным
контактом между телами (теплопроводность,
конвекция), либо лучистым переносом
энергии. Работа представляет собой
иной механизм передачи энергии. В случае
механической работы обязательно
имеет место изменение объема тела.
Теплота - способ
передачи энергии от более нагретого к
менее нагретому телу, величина которого
зависит от процесса передачи энергии.
Как указывалось
ранее, если процесс изохорный, то dqv
= c^dt;
если изобарный, то dqp
= cpdT.
Работа и теплота -
это энергетические характеристики
процесса, механического и теплового
взаимодействия тел, которые существуют
только при протекании процесса, т.е.
они являются функциями процесса.
Внутренняя энергия
Внутренняя энергия
тела и
складывается из энергии поступательного
и вращательного движения молекул
(кинетической энергии) ик,
потенциальной энергии сил сцепления
между молекулами ип,
энергии внутримолекулярных колебаний
ия
и т.д. Т.е. и
= ик
+ ип
+ ия...
Для идеального газа
пренебрегают всеми видами энергии,
кроме кинетической.
Внутренняя энергия
идеального газа является функцией
температуры:
Au
= f(T).
Рассмотрим следующий
пример. К цилиндру подводится теплота
при постоянном объеме (изохорный
процесс).
Согласно первому
закону термодинамики
dq
= du
+ dl.
Работа dl
равна 0, следовательно,
dq
= du.
Элементарное
количество теплоты
dq
= cvdT
= du,
т.е. элементарное изменение внутренней
энергии
du
= cvdT.
Тогда изменение
внутренней энергии при переходе рабочего
тела из состояния 1 в состояние 2:
T2
u1-2
= j cvdT
= cv
(T2
- T1
).
T1
Внутренняя энергия
в отличие от теплоты и работы является
функцией состояния. Т.е. внутренняя
энергия присуща рабочему телу всегда
и характеризует состояние рабочего
тела.
Исходя из рассмотренного
выше, первый закон термодинамики можно
записать следующим образом:
dq
= u
+ pdv
или dq
= c^dT
+ pdv.
У реальных газов,
жидкостей и твердых тел средняя
потенциальная энергия взаимодействия
молекул не равна нулю. Для газов она
много меньше средней кинетической
энергии, но для твердых тел и жидких
тел сравнима с кинетической. Средняя
потенциальная энергия взаимодействия
зависит от объема вещества, так как при
изменении объема меняется среднее
расстояние между молекулами. Следовательно,
внутренняя энергия в общем случае
наряду с температурой зависит и от
объема.
Энтальпия
Важную роль в самых
разнообразных термодинамических
расчетах играет величина, называемая
энтальпией.
Рассмотрим физический
смысл энтальпии.
Рис. 2.12 Физическая
суть энтальгии
На рис. 2.12 показан
цилиндр 1, внутри которого находится
газ 2 (рабочее тело). Объем газа
ограничивается стенками цилиндра и
поршнем 3, находящимся сверху. Поршень
массой m
находится в равновесии и поддерживается
на высоте у
силой, возникающей в результате давления
газа. Полная энергия газа E
равна сумме внутренней энергии газа U
и потенциальной энергии источника
внешнего давления (поршня) Жпот,
т.е. можно записать: E
= U
+ Жпот.
Определим выражение,
с помощью которого можно получить
значение потенциальной энергии внешнего
источника давления Жпот.