Интерполяция. Частотные методы решения задачи интерполяции. Линейный интерполятор на двоичных умножителях частоты.
Интерполяция - восстановление точек кривой по его начальному и конечному значению. Производится в реальном времени, что накладывает определенные условие.
Д
ано:
Xk,
Yk,
Vk;
Найти: fx,
fy
– частоты, которые обеспечивают
равномерное движение по кривой.
;
;
;
;
Линейный интерполятор на ДУЧ
Цепочка четных Т-триггеров;
Любой следующий тактируется фронтом с инвертированного выхода, спадом на нижнем входе;
fвых не может быть больше fвх.
ОВ у любого неинвертированного выхода формирует короткий импульс у фронта любого такта.
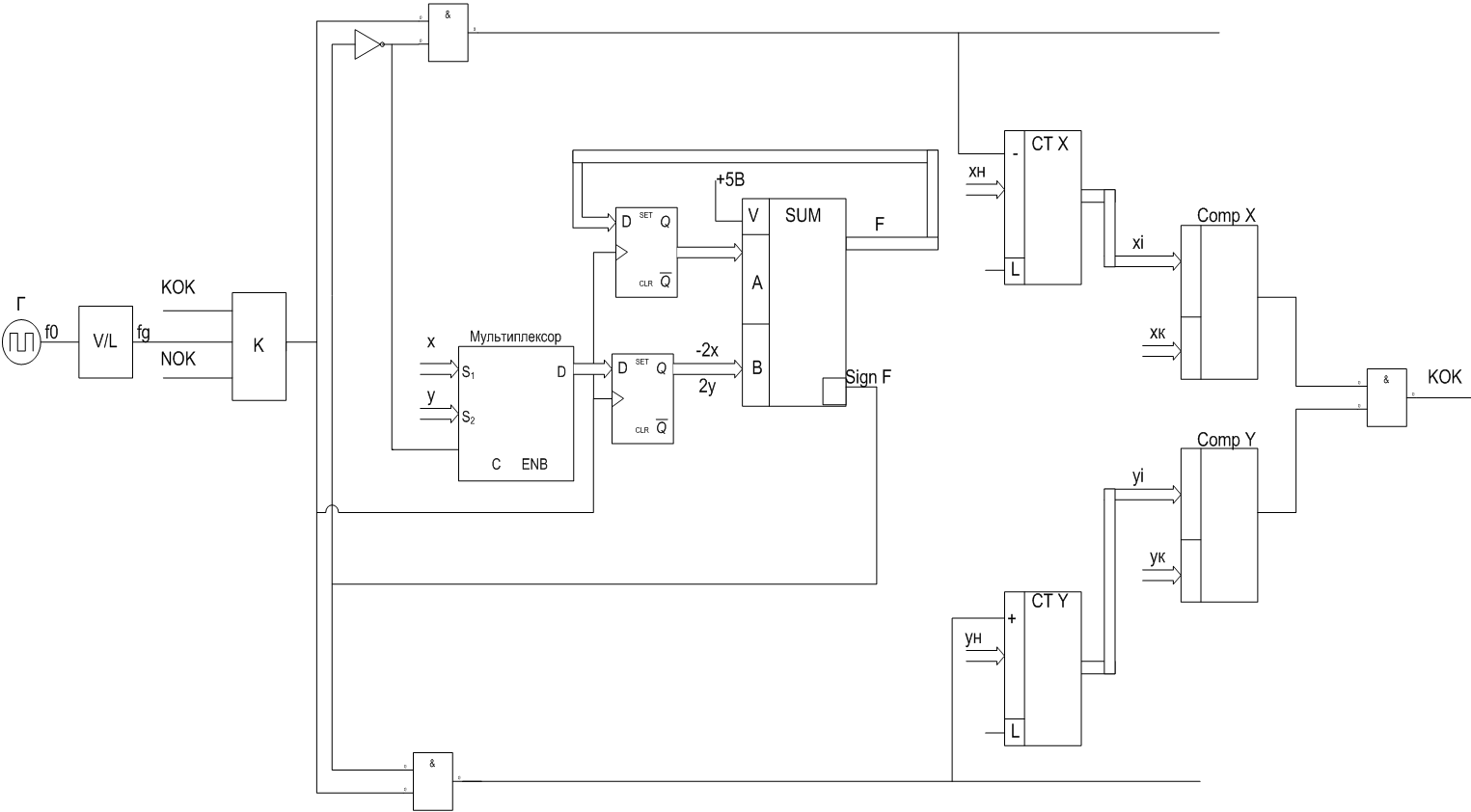
Сам интерполятор:
НОК - начало обработки кадра.
КОК-конец обработки кадра.
К - ключ.
RG x y - регистр, в который записывается координата по х и у.
СТ Х и СТ Y – счетчики по Х и Y соответственно.
Оценочная функция. Линейный интерполятор, использующий оценочные функции.
Т.к.
для интерполятора дискретного действия
функция управления должна быть
кусочно-линейной (
),
то она терпит разрывы в моменты времени,
когда:
;
;
.
Объединим эти условия в уравнение оценочной функции:
Проскочить нельзя, вернуться тоже.
– значение
ОФ.
Шаг
по Х:
Шаг
по Y:
Сумматор используется для определения нового значения ОцФ. Знак ОцФ используется для реализации вычисления одного из уравнений системы. Тригерры (защелки) нужны для захвата переменных на весь временной интервал вычисления. Мультиплексор используется для того, чтобы к предыдущему значению функции в зависимости от ее знака, прибавлять значение х или отрицательное значение у. В зависимости от знака оценочной функции посылается сигнал на х или у.
Отрицательное число нужно представить в дополнительное коде, через инверсию +1.
Оценочная функция. Круговой интерполятор, использующий оценочные функции.
Т.к. для интерполятора дискретного действия функция управления должна быть кусочно-линейной ( ), то она терпит разрывы в моменты времени, когда:
;
;
.
Объединим эти условия в уравнение оценочной функции:
Ее знак покажет, по какой из координат необходимо сделать шаг.
Уравнение траектории для дуги окружности.
Частные производные знака не меняют.
При движении против часовой стрелки
(за траекторией >0, внутри <0):
=
Интерполяция с использованием цда.
Цифровые дифференциальные анализаторы необходимы для решения дифференциальных уравнений в дискретной форме.
;
;
N
– размерность счетчика, f
– частота
счета. Т.о.
.
dev – делитель частоты, sum – сумматор, count – счетчик, compare – компаратор
Решение траекторных задач в микропроцессорных системах. Перечень решаемых задач. Требования к вычислительному устройству.
Вычислительное содержание любой траекторной задачи включает:
• Цифровое моделирование – в реальном масштабе времени – движения изображающей точки (некая абстрактная точка, ставящаяся в соответствие некоторой реальной точке на рабочем органе объекта управления) по заданной в управляющей программе траектории (команды G–движение с постоянным F– заданием или изменяющейся во времени (разгон, торможение), контурной скоростью).
• Разложение вектора контурной скорости Vk(t) на координатные составляющие Vq1(t)… Vqn(t), где индексами qi (i=1..n) отмечены скорости степеней подвижности объекта управления.
• Расчет приращений пути по каждой из координат ∆qi за фиксированный интервал времени (Tk–квант времени): ∆qi=Vqi(t)Tk.
Дополнительные задачи:
• Расчет эквидистанты, т.е. геометрического места точек, равноудаленных от основного контура.
• Ориентация рабочего органа объекта управления относительно программной траектории.
• Прямое и обратное преобразование координат объекта управления в систему координат пользователя.
П
рограммное
на фиксированных интервалах квантования.
Алгебраический метод задач в CNC системах основан на использовании оценочных функций.
Обобщенный алгоритм интерполяции кодовых приращений.
Блок 1. Подготовка данных УП, необходимых для реализации конкретного алгоритма интерполяции, предварительные расчет констант, ввод их в буферные регистры.
Блок 2. Сигнализация о необходимости начать вычисления межтактовых приращений координат, вызов подпрограммы алгоритма интерполяции.
Блок 3. Основной решающий блок. Процесс вычисления приращений координат и промежуточных величин.
Блок 4. Сигнализация о готовности устройства управления приводами координат принять необходимую информацию.
Блок 5. Выдача задающих воздействий на приводы. Увеличение координат на величину межтактовых приращений и проверка условий окончания обработки отрезка траектории, заданного в кадре УП.