1 ПОНЯТИЕ О ПЛАНЕ И КАРТЕ. ПРОФИЛЬ МЕСТНОСТИ

Карта - уменьшенное изображение земной поверхности на плоскости. По содержанию и назначению карты делят на географические карты (это уменьшенное обобщенное, построенное по определенным математическим правилам изображение значительных участков земной поверхности на плоскости с учетом кривизны Земли.) и топографические карты (уменьшенное и обобщенное изображение земной поверхности, передающее размещение и свойства основных природных и социально-экономических объектов местности.).План-изображение на плоскости горизонтальной проекции участка земной поверхности в уменьшенном и подобном виде без учета кривизны Земли. Профилем местности называют уменьшенное изображение вертикального разреза земной поверхности вертикальной плоскостью по данному направлению.

2 ОБРАБОТКА РЕЗУЛЬТАТОВ УГЛОВЫХ ИЗМЕРЕНИЙ В ЗАМКНУТОМ ПОЛИГОНЕ.

Расчеты: 1.отсчитывают сумму измеренных углов (∑_{β изм.}) 2. подсчитывают теоретическую сумму ∑_{β теор}=180(n-2) (n - количество углов) 3. высчитывают угловую невязку (плюс или минус) f_βвыч. = ∑_{β изм} - ∑_{β теор} 4.высчитывают допустимую невязку, в минутах f_{β доп.} =±1,5* . 5. полученную невязку сравнивают с допустимой- если невязка не выходит за пределы допустимой, то проводят вычисления. Если невязка выходит за пределы, то проверяют вычисления. Или необходимо перемерить углы в поле. Если невязка допустима, то ее сразу поровну распределяют на все углы, т.е. в углы вводят поправку. Поправку вводят со знаком обратным знаку невязки. Если поправка не велика, то поправку вводят преимущественно в острые углы, или в углы между самыми короткими сторонами.6. в поле мы измеряем А_м сторон – изменчивая величина, поэтому делаем пересчет на дирекционные углы α. α_1-2-дано, α_2-3=180°+α_1-2-β₂ (β-исправленный). Если α>360°, следует вычесть 360°, если после прибавлении 180° к α, β_исп. не вычитается из него, то необходимо прибавить еще 360°.7. Румбы-определяем в какой четверти находится линия по α. Для I ч: r₁ =α ₁,СВ, для II ч: r ₂ = 180°-α ₂ ЮВ, для III ч: r ₃ = α ₃ -180° ЮЗ, для IV ч: r₄ = 360° -α ₄ СЗ.

3 СУЩНОСТЬ И СПОСОБЫ ГЕОМЕТРИЧЕСКОГО НИВЕЛИРОВАНИЯ

Нивелирование-вид геодезических работ, в результате которых определяют превышение точек земной поверхности, а также высоты этих точек над принятой уровенной поверхностью. Один из методов нивелирования - геометрическое нивелирование, которое заключается в непосредственном определении превышения одной точки над другой. Его выполняют с помощью специального инструмента-нивелира, приспособленного для визирования в горизонтальном направлении, и нивелируемых реек, устанавливаемых вертикально в нивелируемых точках. Различают 2 способа геометрического нивелирования:1)нивелирование из середины. 2)нивелирование вперед.

4 МАСШТАБ ПЛАНОВ И КАРТ. ТОЧНОСТЬ МАСШТАБОВ

Масштаб-степень уменьшения длин линий на планах и картах по отношению к горизонтальным проекциям этих линий на местности. Бывают численные (всегда выражаются дробью , 1:N, где в числителе всегда единица, а знаменатель показывает, во сколько раз уменьшены горизонтальные проекции линий местности при переносе их на план.) и графические масштабы. Графические масштабы делятся на линейный(представляет собой диаграмму, на которой несколько раз отложены отрезки обычно по 1 см, называемые основанием масштаба, а крайнее левое основание разделено на 10 одинаковых частей, равных 1 мм.) и поперечный(диаграмма, позволяющая откладывать линии без пересчета, более точный из масштабов, его мы строили.). Масштаб плана и карты- один из основных показателей карт. Точность-такое горизонтальное проложение (проекция) линий местности, которое на бумаге изображается отрезком 0,1 мм. (пример: М 1:500, его точность(в метрах) 0,1 мм=0,05м, М 1:1000, его точность=0,1м.)

5 ВЫЧИСЛЕНИЕ И УВЯЗКА ПРИРАЩЕНИЙ ПРЯМОУГОЛЬНЫХ КООРДИНАТ ТОЧЕК В ЗАМКНУТОМ ПОЛИГОНЕ

Координаты каждой последующей точки будут равны координатам предыдущей точки ± приращение координат. Формула для расчета приращений: ∆x= |d*cos α| =|d*cos r| , ∆y=|d*sin α| =|d*sin r|. (α-дирекционный угол, r- румб,d – горизонтальное проложение.) Приращение зависит от четверти (отрицат.,или положит): СВ(∆x+, ∆y+), ЮВ(∆x-, ∆y+), ЮЗ(∆x-,∆y-), СЗ(∆x+,∆y-).Вычисление увязки приращения координат: 1)подсчитываем алгебраическую сумму ∆x и ∆yс учетом знаков: f_x=∑∆x, f_y=∑∆y. 2)теоретическая сумма приращения по оси x и y в замкнутом полигоне равен нулю. Из-за неизбежных ошибок при измерениях и вычислениях это условие не выполняется и ∑ приращения координат будут являться невязками. _{s= x}² + _y² . (невязка по оси x (f_x) и по оси y (f_y), линейная невязка (f_s)). Допустимость этой линейной невязки определяется относительной невязкой, зависящей от точности линейных измерений. f_отн.= f_s / P_{(периметр)}. Допустимая невязка . Если относительная невязка меньше допустимого значения, то полученные невязки f_x и f_y распределяют в виде поправок соответственно на все приращения. Величина поправок

пропорциональны длинам сторон, т.е.горизонтальным проложениям. (чем больше сторона, тем больше поправка). S _xi =f_x / P * d_i .Знак поправки обратный знаку невязки.

6. НИВЕЛИРОВАНИЕ «ВПЕРЕД»

Нивелирование – вид геодезических работ, в результате которых определяют превышение точек земной поверхности, а также высоты этих точек над принятой уровенной поверхностью. Геометрическое нивелирование заключается в непосредственном определении превышения одной точки над другой. Его выполняют с помощью специального инструмента – нивелира, приспособленного для визирования в горизонтальном направлении, и нивелируемых реек. Существует два способа геометрического нивелирования: из середины и вперед. Нивелирование вперед. Для получения повышения h можно поставить нивелир окуляром над точкой А местности и сделать при горизонтальном положении визирной оси отсчет b. Кроме того, нужно измерить высоту инструмента I (высоту визирной оси над точкой А.)

Тогда согласно рисунку б h=i-b

Hb = Ha + h

Такое нивелирование называют нивелированием вперед. При нивелировании вперед взгляд назад заменяют высотой инструмента i. Из рисунка в видно, что если нивелир поставить выше (или ниже) то оба отсчета изменятся на одно и тоже значение по сравнению с ранее сделанными отсчетами а и б и разности отсчетов а-б будут одинаковыми ( т.е одинаковыми будут значения превышения точек – h. Для вычисления отметок нескольких точек можно применить способ горизонта инструмента. ГИ - это высота луча визирования над уровенной поверхностью

7. СИСТЕМЫ КООРДИНАТ, ПРИМЕНЯЕМЫЕ В ГЕОДЕЗИИ

Положение точек физ. поверхности Земли может быть определено с помощью системы координат. Координаты – величины (числа), заданием которых определяется положение точки на плоскости, на любой поверхности или в пространстве. В геодезии наибольшее распространение получили : географическая, плоская прямоугольная, зональная, полярная системы координат.

Географические координаты – угловые величины (широта и долгота), определяющие положение точки на земном шаре. Земля вращается вокруг оси, концы которой называются полюсами Рс – северный и Рю – южный. Плоскость, перпендикулярная оси Земли и проходящая через центр сфероида, называют плоскостью земного экватора, а линию пересечения её с поверхностью земли – экватором QQ1. Точка пересечения земной оси с плоскостью экватора называется центр земли. Параллели – линии пересечения Земли с плоскостями II плоскости экватора. Меридианы – линии пересечения Земли с плоскостями, проходящими через ось вращения земли. Широта Ф – угол, составленный отвесной линией через данную точку и плоскостью экватора. (0^о-90^о) С.Ш. – «+», Ю.Ш. – «-» ( QE Q1E). Долгота λ - двугранный угол, образованный плоскостью нулевого меридиана и меридиана проходящего через данную точку. (0^о-180^о). Нулевой меридиан установились считать меридиан, проходящий через обсерваторию в Гринвиче вблизи Лондона. Географические координаты точек земной поверхности определяют путем астрономических наблюдений.

Прямоугольные координаты. Они нашли широкое применение в геодезии при использовании топографических карт. В системе прямоугольных координат положение каждой точки определяется расстоянием от взаимно перпендикулярных осей, лежащих в горизонтальной плоскости. За ось Х принята вертикальная линия, совпадающая с направлением север – юг( не как в мы привыкли а наоборот). За положительное направление принято направление на север(верх) и на восток (вправо). Оси разделяют на четыре четверти, 1 – северо-восточная, 2 – юго – восточная, 3 –юго-западная, 4 северо- восточная. При произвольном выборе осей подобную систему координат называют частной. Её используют в инженерно-геодезических работах на небольших территориях.

Зональная система координат. В нашей стране топографические карты построены в картографической поверхности Гаусса – Крюгера, в которой земной эллипсоид изображают виде шестиградусных меридиальных зон. В каждой зоне средний меридиан называют осевым. Осевой меридиан и экватор изображают прямыми взаимно перпендикулярными линии. Их принимают за оси прямоугольных координат мередиан – за ось Х, экватор – за ось У. Счет абсцисс ведут от экватора к полюсам. Чтобы не иметь дела с отрицательными значениями ординат, которые усложняют расчеты, условно принимают орбиту начала координат равной +500км. При этом самая западная точка любой зоны будет иметь ординату примерно + 165км. Земной шар разбит 60 шестиградусных зон. 1 зона составляет 6^о. Каждая зона имеет долготу (6^о п – 3^о). Для удобства пользования на каждый лист наносят координатную сетку.ю образованную прямыми линиями, параллельными осями абцисс и ординат. Координатные линии проводят через определенное число километров. Координаты линий, ближайших к углам подписывают полностью, остальные – сокращенно, последними двумя цифрами километров, такую сетку называют километровой.

Полярные координаты могут быть применены при составлении карт и планов небольших участков местности. Если потожение точки О(начала координат) известно то определив от некоторого начального направления ON уголβ до направления на точку M и отложив вдоль него расстояние до этой точки D, получим положение точки М. В топографии за начальное направление принимают северные направления меридианов : географического магнитного или осевого проекции Гаус-крюгера ( вертикальную линию сетки). В зависимости от того, какое из этих направлений принято за начальное, угломβ будут: азимут, магнитный азимут, дирекционный угол α.

8 СПОСОБЫ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ

Аналитический способ. Если участок представляет собой замкнутый многоугольник, то, сняв с плана прямоугольные координаты его вершин, площадь участка вычисляют по формуле:

,

где i - номера вершин многоугольника, пронумерованных по ходу часовой стрелки.

По этой же формуле можно вычислить площадь с криволинейными границами, если координаты точек границы сняты так часто, что отрезки между точками можно считать прямыми. В последнем случае съём координат выполняют с помощью специального прибора – дигитайзера, а вычисления выполняют на ЭВМ.

Графические способы. Участок на плане разбивают на простые геометрические фигуры (обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют.

Разбиение площади на простые фигуры выполняют также, применяя палетки. Палетка - лист прозрачного материала (восковки, лавсана, пластика), на который нанесена сетка квадратов размером 2×2 мм или система равноотстоящих параллельных линий. Наложив палетку с квадратами на план, подсчитывают число квадратов, уместившихся в измеряемой площади, оценивая дробные части квадратов на краях участка на глаз. Результат подсчёта умножают на площадь одного квадрата.

Палеткой с параллельными линиями площадь делится на трапеции, в каждой из которых измеряют длину средней линии. Суммируя площади трапеций, равные произведению длины средней линии на расстояние между линиями, определяют площадь участка.

Точность определения площади с помощью палеток - 1/50.

Полярный планиметр. Планиметрами называются приборы для измерения площадей. Наиболее распространён полярный планиметр (рис. 4.11). Он состоит из двух рычагов – полюсного 1 и обводного 4, соединяемых шарниром 8. Полюс планиметра (массивный цилиндр 2 с иглой, втыкаемой в бумагу) в процессе измерения площади остается неподвижным. На конце длинного плеча обводного рычага укреплен шпиль 3 (или лупа с маркой в виде креста в ее центре), которым обводят контур измеряемой площади. На коротком плече обводного рычага крепится каретка с мерным колесиком 6, опирающимся на поверхность бумаги, и счетным механизмом. Когда обводной шпиль 3 (или марка) перемещается по линии контура перпендикулярно рычагу, мерное колесико 6 катится по бумаге. При перемещении обводного шпиля по направлению рычага колесико скользит по бумаге, не вращаясь. При перемещении шпиля в иных направлениях происходит и вращение, и скольжение. Суммарное число оборотов колесика, накопленное при обводке шпилем контура, пропорционально площади, ограниченной контуром.

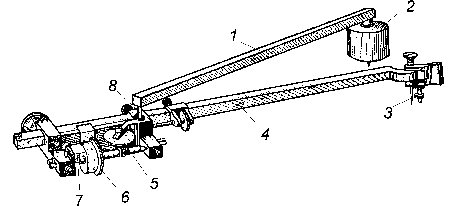
Рис. 4.11. Полярный планиметр

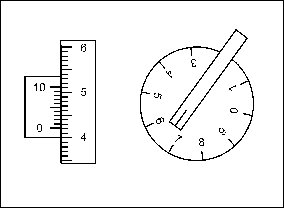
Для подсчета числа оборотов вращение колесика передается на циферблат 5. По ободу колесика нанесено 100 делений. Отсчеты по шкале обода берут с помощью верньера 7. Отсчет по планиметру (рис. 4.12) состоит из отсчета числа целых оборотов колесика по циферблату (на рисунке – цифра 6), отсчета десятых и сотых долей оборота - по шкале обода против нуля верньера (цифры 4 и 2) и тысячных долей оборота – по номеру штриха верньера, совпадающего со штрихом на шкале обода (цифра 2).Для измерения площади, обводят её контур, делая при этом два отсчёта по планиметру: один n₁ - до обвода, другой n₂ - после. Площадь вычисляют по формуле S = c·(n₂ - n₁) , (4.3)

где c – цена деления планиметра. Для надёжности площадь измеряют 3 - 5 раз и полученные результаты осредняют.Если во время измерений полюс планиметра располагался внутри измеряемой площади, то вместо формулы (4.3) используют формулуS = c·(n₂ - n₁ + Q) ,

где Q - постоянная планиметра.

- 6422

 Цена деления планиметра c зависит от длины обводного рычага и регулируется перемещением по нему каретки с мерным колёсиком и счётным механизмом. Перед измерением площади цену деления планиметра определяют. При этом, расположив полюс в стороне, обводят фигуру, площадь S₀ которой известна (например, квадрат километровой сетки на карте) и вычисляют цену деления с = S₀ /(n₂ - n₁).

Для определения постоянной Q обводят фигуру с известной площадью, поместив полюс внутри этой площади, после чего вычисляют Q = (S₀ /c) - (n₂ - n₁).

Точность определения площади планиметром - 1/300.

Электронные планиметры. Электронный полярный планиметр устроен подобно механическому, но имеет электронное счетное устройство и жидкокристаллический дисплей.

Электронный роликовый планиметр катится на двух высокофрикционных абразивных роликах, измеряющих смещения по направлению качения. Поворотная штанга с курсором, перемещаемым по контуру площади, измеряет смещения в поперечном направлении. Счетное устройство вычисляет площадь и высвечивает ее величину на дисплее.

Электронный роликовый планиметр-дигитайзер позволяет, кроме измерения площади, снимать координаты точек и решать некоторые задачи – определение радиуса окружности, длины дуги, площади сегмента и др. Возможна связь с компьютером через стандартный интерфейс.

9. ВЫЧИСЛЕНИЕ ОТМЕТОК ТОЧЕК ПРОЕКТНОЙ ЛИНИИ ПРОДОЛЬНОГО ПРОФИЛЯ ТРАССЫ.

Вычисление отметок точек через превышение. Разность высот точек Нв – На – превышение h, поэтому если известна отметка точки А (На), то отметка точки В (Нв) определяется по методу превышения: Нв = На + h.

Вычисление отметок точек через горизонт инструмента. Отметку горизонтального луча называют горизонтом инструмента. Hi = Ha + a, тогда Hb = Hi – a, т.е отметка горизонта инструмента равна горизонту инструмента на этой точке. Вычисление отметок точек через ГИ широко применяется в практике для определения отметок нескольких точек с одной установки нивелира (например, при нивелировании поверхности по квадратам). Вычитая из Hi отсчет b по рейке, поставленной в искомой точке B, получают отметку Hi последней. Ha = a+ Hi Hi – b = Hb

10 УСЛОВНЫЕ ЗНАКИ НА ТОПОГРАФИЧЕСКИХ КАРТАХ И ПЛАНАХ

Условные обозначения – графические символы для изображения предметов, объектов и рельефа местности на картах и планах. Требования : наглядность и компактность. Все условные знаки можно разделить на 4 группы: масштабные, внемасштабные, линейные, пояснительные.

Масштабные служат для изображения крупных объектов местности, имеющих ярко выраженные контуры, размеры и площадь которых значительно превышает точность масштаба (луг, лес, пашня, озеро), Контуры обозначаются точечной или сплошной линией.

Внемасштабные изображают объекты местности и предметы, имеющие важное значение для ориентира, но малые размеры, так что их нельзя изобразить в масштабе (колодец, мельница, завод, пункт триангуляции).

Пояснительные раскрывают содержание объекта и дают его характеристику (цифры подписи) – направление реки, ширина дороги.

Линейные – дороги средства связи, линии электропередач занимают особое положение, т.к их длину можно изобразить в масштабе, а ширину нет .

11.Решение прямой геодезической задачи.

По координатам начала отрезка прямой, по длине и направлению нужно найти координаты конца отрезка;

Зная координаты Х₁ и У₁ точки 1,диррекционный угол а_1-2 на точку 2 и расстояние d_1-2 до нее ,найти координаты Х₂ и У₂ точки 2 .

Х₂=Х₁+(Х₁-Х₂)=Х₁+дельта Х;

У₂=У₁+(У₁-У₂)=У₁+дельта У.

Разности координат дельта Х и дельта У называют приращение координат .

Х₂-Х₁=дельта Х=d_1-2 cos а_1-2;

У₂-У₁=дельта У=d_1-2 sin а_1-2

12.Продольное и поперечное нивелирование трассы.Нивелирный журнал.

Если объект строительства занимает узкую, длинную полосу ,то нивелируют трассу -ось предполагаемого будущего сооружения ,такое нивелирование наз.продольным.

На основании продольного нивелирования вычисляют высоты пронивелированных точек и затем составляют продольный профиль трассы.

Трасса-это линия,определяющая путь движения или продольную ось дороги, канала, линии электропередачи и связи и подобных сооружений большой протяженности.

при продольном нивелировании на линии хода разбивают пикетаж,т.е. на местности намечают и закрепляют через каждые 100 м. точки ,наз.пикетами.

После закрепления точек на линии хода приступают к их нивелированию

При двустронних рейках каждую пару соседних пикетных точек нивелируют по способу из середины по двум сторонам реек .Плюсовые тиочки нивелируют только по рабочей(черной)стороне.

Способ поперечников.

Это способ,используемый при съемке притрассовой полосы,вдоль трасс автомобильных дорог ,каналов и др. линейных объектов.

Планово-высотным обоснованием в этом случае явл. трасса линейного оъекта,т.е. теодолитно нивелирный ход.

С помощью угломерного прибора и ленты или рулетки через определенные расстояния разбивают поперечники. Их разбивают на пикетных и плюсовых точках, высоты которых уже определены в результате продольного нивелирования.

это один из способов геометрического нивелирования поверхности.

14. Теодолитная съемка. Способ перпендикуляров.

Теодолитная съемка-это горизонтальная съемка по результатам кот. составляют контурный план местности .Для этого на местности необходимо иметь опорные точки и линии от кот. и производятся детальные измерения.

Сеть таких опорных точек наз. съёмочным обоснованием ,поэтому полевые работы при теодолитной съемке организовываются так, чтобы в первую очередь произвести измерения, обеспечивающие получение координат опорных точек.

Этапы теодолит съемки:

1.Камеральная подготовка материалов.

2.Рекогносцировка местностей и закрепление опорных точек.

3.Полевые геодезические работы.

4.Камеральная обработка результатов измерений.

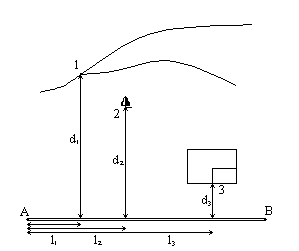
Способ перпендикуляров (прямоугольных координат) для съемки контуров лежащих вблизи теодолитного хода. Линию теодолитного хода 1–2 (рис. 9.1) принимают за ось абсцисс с началом в задней точке 1. На этой оси с помощью экера (при небольших расстояниях – на глаз) к характерным точкам ситуации (р. Каменный, рис. 9.1)строят перпендикуляры (ординаты), длины которых измеряют мерной лентой. Таким образом, имея значения абсциссы и ординаты, наносят эту точку на план.

Способ перпендикуляров. Способ перпендикуляров является реализацией обычной прямоугольной системы координат. Пусть линия АВ - одна из сторон теодолитного хода. Примем ее за ось l, начало координат совместим с пунктом А; ось d расположим перпендикулярно линии АВ. Положение точки 1 определяется двумя перпендикулярами l1 и d1, длины которых измеряют мерной лентой или рулеткой.