Билет 9

Аффинные преобразования. Уравнения картографических проекций. Итерационные методы преобразования координат. Ресэмплинг.

Определение аффинных преобразований

Давайте поговорим о растяжениях и сжатиях плоских фигур.

Если растянуть вдоль какого-то направления круг, то получится лекальная кривая - эллипс.

Если растянуть квадрат в направлении, параллельном одной паре сторон, то получится прямоугольник. Если же квадрат растянуть или сжать в направлении его диагонали, то получится параллелограмм.

Растяжения и сжатия, о которых мы будем говорить, в определенном смысле, равномерные.

Эта равномерность означает, что все кусочки плоскости будут растягиваться (сжиматься) одинаково.

Кроме того, когда мы растягиваем (сжимаем) квадрат, его стороны -- отрезки остаются отрезками.

Такие равномерные растяжения (сжатия) называются аффинными преобразованиями.

Преобразование плоскости называется аффинным, если оно взаимно однозначно и образом любой прямой является прямая. Преобразование называется взаимно однозначным, если оно разные точки переводит в разные, и в каждую точку переходит какая-то точка.

Напомним, что преобразование -- это отображение множества на само себя. Отображение называется взаимооднозначным (биективным), если разные элементы переходят в разные, и в каждый элемент переходит какой-то элемент.

Частным случаем аффинных преобразований являются просто движения (без какого-либо сжатия или растяжения). Движения — это параллельные переносы, повороты, различные симметрии и их комбинации.

Другой важный случай аффинных преобразований — это растяжения и сжатия относительно прямой.

На рисунке 1 показаны различные движения плоскости с нарисованным на ней домиком. А на рисунке 2 показаны различные аффинные преобразования этой плоскости.

Рисунок 1. Примеры движений.

Рисунок 2. Примеры аффинных преобразований.

Обозначим множество движений плоскости как  , а множество аффинных преобразований как  . Тогда верно следующее утверждение.

Определение 2.

Множество движений есть подмножество множества аффинных преобразований.

Доказательство.

Это кажется очевидным. Давайте поймем, что нам собственно нужно доказать. Для этого нужно ещё раз посмотреть на определения движения и аффинных преобразований. Нужно доказать, что любое движение является аффинным. То есть нужно показать, что при движении разные точки переходят в разные, и образ любой прямой есть прямая.

Это интуитивно ясно — при движении фигуры вообще не меняют своей формы и размеров, а меняют лишь своё положение на плоскости. Также и прямые будут сохранять свою форму — оставаться прямыми. Движение можно представлять как перемещение листка бумаги с рисунком по парте. При движении разные точки остаются разными, поскольку расстояния сохраняются. Если точки были «разделены» некоторым расстоянием, то и после движения они будут «разделены» этим же расстоянием.

Конец доказательства.

Растяжения и сжатия

Определение 3. Растяжением плоскости относительно прямой   с коэффициентом   называется преобразование плоскости, при котором каждая точка   переходит в такую точку  , что расстояние от прямой   до   в   раз больше, чем до точки  , и проекция точек   и   на прямую   совпадают. Если коэффициент   положительный, то точки   и   лежат по одну сторону от прямой  , если отрицательный — то по разные.

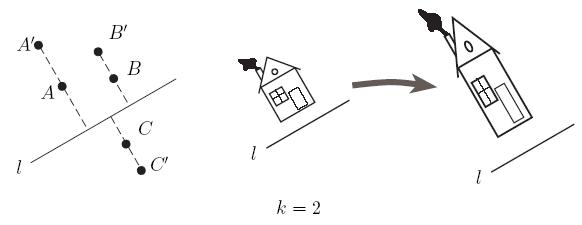
Рисунок 3. Сжатия и растяжения относительно прямой.

Давайте докажем, что растяжение (сжатие) относительно прямой является аффинным преобразованием. Во-первых, эти преобразование взаимно однозначно. Чтобы доказать это заметим, что для каждого сжатия есть растяжение, которое все точки возвращает на свои места, и наоборот, для каждого растяжения есть возвращающее всё на свои места сжатие. А сейчас воспользуемся теоремой:

Теорема 1

Если преобразование   обратно преобразованию  , а преобразование   обратно преобразованию  , то   и   взаимно однозначные преобразования.

Определение 4.

Преобразование   называется обратным к преобразованию  , если преобразование  , применённое после преобразования  , все точки возвращает на свои места. Если преобразование   точку   переводит в точку  , то обратное преобразование точку   переводит в точку  .

Утверждение 2.

Растяжение (сжатие) относительно прямой есть аффинное преобразования.

Доказательство.

Нам осталось показать, что сжатие и растяжение прямые переводят в прямые. Пусть растяжение осуществляется относительно прямой  . Направим вдоль неё ось  . Рассмотрим любую прямую  . Возможны два случая.

1) Если она пересекается с  , то проведем через точку пересечения ось  , перпендикулярную  . Тогда уравнение прямой   будет иметь вид:

При растяжении относительно прямой   (оси  ) с коэффициентом   точка   переходит в точку  :

растяжение относительно оси 'X' : 

Точка   прямой   перейдёт в точку с координатами  . А значит, координаты новых точек будут удовлетворять уравнению

— это уравнение прямой. Итак образы точек прямой   лежат на прямой  .

2) Если она не пересекается с  .

Задача 13.1[9] Случай, когда   не пересекается с  , рассмотрите самостоятельно.

Решение.

Если   не пересекается с  , то все точки   удалены от прямой   на определенное расстояние  . После сжатия или растяжения относительно   они станут точками, удалёнными от прямой на расстояние   и по прежнему будут лежать по одну сторону от прямой  . А значит, они будут лежать на прямой.

Конец решения.

Конец доказательства.

Итак, кроме движений плоскости аффинные преобразования содержат еще сжатия и растяжения относительно прямой. Если мы применим растяжение относительно одной прямой, а потом относительно другой прямой, то снова получим аффинное преобразование, так как и первое, и второе растяжение сохраняло прямые и разные точки переводило в разные. Вообще верно

Утверждение 3

Композиция аффинных преобразований есть снова аффинное преобразование:

Мы здесь использовали значок « » композиции. Выражение   следует понимать как преобразование плоскости, которое получается после применения преобразования   и последующего применения преобразования  . Значок « » следует читать как «принадлежит», то есть «содержатся внутри как элемент».

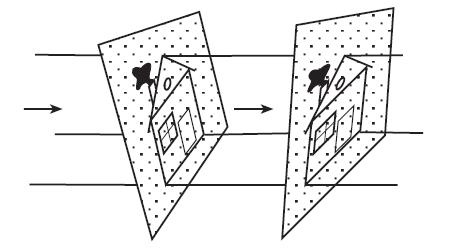
Рисунок 4. При параллельном проектировании с одной плоскости на другую фигура подвергается растяжению (сжатию) относительно прямой пересечения плоскостей.

Задача 2[10]

Докажите, что при параллельной проекции фигуры с одной плоскости на другую, фигура на второй 1) совпадает с тем, что изображено на первой, если плоскости параллельны; 2) является растяжением (сжатием) того, что изображено на первой плоскости, относительно прямой пересечения плоскостей, если плоскости пересекаются.