
- •21. Потенциальная энергия
- •22. Внутренняя энергия. Полная энергия
- •25.Работа и мощность силы
- •26. Закон сохранения импульса. Следствие
- •27. Закон сохранения момента импульса. Следствия
- •28. Закон сохранения энергии. Следствия
- •29. Основной закон динамики поступательного движения
- •32. Гравитационное взаимодействие
- •33. Электромагнитное взаимодействие
- •№42 Напряжённость электрического поля
- •Поток вектора напряженности электростатического поля
- •54. Основные уравнения электромагнетизма – уравнение Максвелла
- •Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
32. Гравитационное взаимодействие
Гравитационное взаимодействие - фундаментальное дальнодействующее взаимодействие. В отличие от электромагнитного взаимодействия, при Г.в. возможно только притяжение, зависящее от массы частиц и расстояния между ними. Г.в. - наиболее универсальное: ему подвержены все частицы, поля, волны. В то же время, на уровне микромира оно самое слабое и во взаимодействиях элементарных частиц практически не проявляется. Г.в. становится заметным на макроуровне, а на мегауровне - там, где скапливаются большие массы, - оно становится преобладающим. Движение небесных тел, а также элементарных частиц, движущихся в космических гравитационных полях со скоростями порядка 1000 км/с и менее, практически полностью определяется Г.в.
33. Электромагнитное взаимодействие
Электромагни́тное взаимоде́йствие — одно из четырёх фундаментальных взаимодействий. Электромагнитное взаимодействие существует между частицами, обладающими электрическим зарядомHYPERLINK "http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D0%BE%D0%B5_%D0%B2%D0%B7%D0%B0%D0%B8%D0%BC%D0%BE%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D0%B5"[1]. С современной точки зрения электромагнитное взаимодействие между заряженными частицами осуществляется не прямо, а только посредством электромагнитного поля.
Электромагнитное взаимодействие отличается от слабогоHYPERLINK "http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D0%BE%D0%B5_%D0%B2%D0%B7%D0%B0%D0%B8%D0%BC%D0%BE%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D0%B5"[3] и сильногоHYPERLINK "http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D0%BE%D0%B5_%D0%B2%D0%B7%D0%B0%D0%B8%D0%BC%D0%BE%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D0%B5"[4] взаимодействия своим дальнодействующим характером — сила взаимодействия между двумя зарядами спадает только как вторая степень расстояния (см.: закон Кулона). По такому же закону спадает с расстоянием гравитационное взаимодействие. Электромагнитное взаимодействие заряженных частиц намного сильнее гравитационного. В классических рамках электромагнитное взаимодействие описывается классической электродинамикой.
34. Гравитационное поле. Свойства. Закон всемирного тяготения
Гравитационное поле, или поле тяготения — физическое поле, через которое осуществляется гравитационное взаимодействие.
Согласно закону всемирного тяготения Ньютона сила гравитационного взаимодействия Fg двух точечных масс m1 и m2 равна
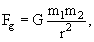
G = 6.67·10-11 м3· кг–1·см–2 − гравитационная постоянная, r − расстояние между взаимодействующими массами m1 и m2.
Фундаментальное свойство гравитационного поля состоит в том, что оно определяет геометрию пространства-времени, в котором движется материя.
35. Напряженность гравитационного поля. Принцип суперпозиции для гравитационных полей
Напряжённость гравитационного поля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела:
![]()
принцип суперпозиции: гравитационное поле двух материальных точек (или тел) равно сумме гравитационных полей каждой из этих точек (или тел) по отдельности. Иначе говоря, силы тяготения не экранируются.
Согласно
принципа суперпозиции, гравитационный
потенциал ![]() точек
равен сумме гравитационных потенциалов
всех точек
точек
равен сумме гравитационных потенциалов
всех точек
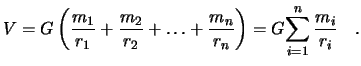
Если точек бесконечное число, а массы их бесконечно малы, то имеем дело с интегральной суммой, и нашу формулу следует записать так
|
|
где ![]() --
расстояние
между фиксированной точкой
--
расстояние
между фиксированной точкой ![]() и
элементом притягивающей массы
и
элементом притягивающей массы ![]() .
.
Пусть ![]() ,
, ![]() ,
, ![]() --
координаты точки
,
а
--
координаты точки
,
а ![]() ,
, ![]() ,
, ![]() --
координаты текущей точки с массой dm тогда
формулу (3.3)
можно переписать следующим
образом м
--
координаты текущей точки с массой dm тогда
формулу (3.3)
можно переписать следующим
образом м
36. Поток вектора напряженности гравитационного поля. Теорема Гаусса Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей. Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния] в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически). В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике. Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхностиэлектрическомуHYPERLINK "http://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B7%D0%B0%D1%80%D1%8F%D0%B4" заряду.
37. Потенциал гравитационного поля Энергия потенциального взаимодействия двух тел массами m и M, находящимися на расстоянии r друг от друга, определяется уравнением
Если частица с массой m находится вблизи нескольких тел, то ее потенциальная энергия W равна алгебраической сумме энергий взаимодействия с каждым из тел по-отдельности. При этом отношение энергии W к величине массы m частицы является функцией положения частицы в пространстве и может рассматриваться в качестве скалярного поля φ, называемого потенциалом гравитационного поля. Потенциал гравитационного поля, образованного частицей с массой M в точке, расположенной на расстоянии r, описывается уравнением
Потенциал
гравитационного поля равен потенциальной
энергии частицы единичной массы:
|
38. Гравитационное поле точечной массы
Гравитацио́нный
потенциа́л — скалярная функция координат и времени,
характеризующая гравитационное
поле в классической
механике.
Имеет
размерность квадрата скорости, обычно
обозначается буквой ![]() .
Гравитационный
потенциал равен отношению потенциальной
энергии материальной
точки,
помещённой
в рассматриваемую точку гравитационного
поля,
к массе этой
точки.
.
Гравитационный
потенциал равен отношению потенциальной
энергии материальной
точки,
помещённой
в рассматриваемую точку гравитационного
поля,
к массе этой
точки.
39. Электромагнитное поле. Свойства
Электромагни́тное по́ле — фундаментальное физическое поле, взаимодействующее с электрически заряженными телами.
Электромагнитное поле (и его изменение со временем) описывается в электродинамике в классическом приближении посредством системы уравнений Максвелла. При переходе от одной инерциальной системы отсчета к другой электрическое и магнитное поле в новой системе отсчета — каждое зависит от обоих — электрического и магнитного — в старой, и это ещё одна из причин, заставляющая рассматривать электрическое и магнитное поле как проявления единого электромагнитного поля.
Действие электромагнитного поля на заряженные тела описывается в классическом приближении посредством силы Лоренца.
40. Электрический заряд. Свойства
Электрический заряд - это физическая величина, определяющая интенсивность электромагнитных взаимодействий.
Единица заряда - [q] кулон.
Свойства электрического заряда :
1. Электрический заряд не является знакоопределенной величиной, существуют как положительные, так и отрицательные заряды.
2. Электричесий заряд - величина инвариантная. Он не изменяется при движении носителя заряда.
3. Электричесий заряд аддитивен.
4. Электричесий заряд кратен элементарному. q = Ne. Это свойство заряда называется квантованностью.
5. Суммарный электричесий заряд всякой изолированной системы сохраняется. Это свойство есть закон сохранения электрического заряда.
№41 Взаимодействие зарядов. Закон Кулона
И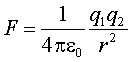 звестно,
что одноименные заряды отталкиваются,
разноименные - притягиваются. Закон
взаимодействия зарядов впервые
сформулировал Кулон в 1785 г Зако́н
Куло́на —
это закон,
описывающий силы взаимодействия между точечными
электрическими зарядами.
q1, q2 -
взаимодействующие заряды,
r -
расстояние между зарядами.
звестно,
что одноименные заряды отталкиваются,
разноименные - притягиваются. Закон
взаимодействия зарядов впервые
сформулировал Кулон в 1785 г Зако́н
Куло́на —
это закон,
описывающий силы взаимодействия между точечными
электрическими зарядами.
q1, q2 -
взаимодействующие заряды,
r -
расстояние между зарядами.
![]() ≈ 8,854187817·10−12 Ф/м — электрическая
постоянная.
≈ 8,854187817·10−12 Ф/м — электрическая
постоянная.
В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:
![]()
где ![]() —
сила, с которой заряд 1 действует на
заряд 2;
—
сила, с которой заряд 1 действует на
заряд 2; ![]() —
величина зарядов;
—
величина зарядов; ![]() —
радиус-вектор (вектор, направленный от
заряда 1 к заряду 2, и равный, по модулю,
расстоянию между зарядами —
—
радиус-вектор (вектор, направленный от
заряда 1 к заряду 2, и равный, по модулю,
расстоянию между зарядами — ![]() );
); ![]() —
коэффициент пропорциональности. Таким
образом, закон указывает, что одноимённые
заряды отталкиваются (а разноимённые —
притягиваются).
—
коэффициент пропорциональности. Таким
образом, закон указывает, что одноимённые
заряды отталкиваются (а разноимённые —
притягиваются).
![]() ≈ 8,854187817·10−12 Ф/м — электрическая
постоянная.
≈ 8,854187817·10−12 Ф/м — электрическая
постоянная.

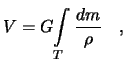
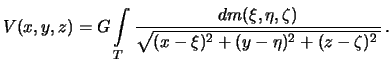
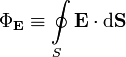 —
поток
вектора напряжённости электрического
поля через замкнутую поверхность
—
поток
вектора напряжённости электрического
поля через замкнутую поверхность