
- •21. Потенциальная энергия
- •22. Внутренняя энергия. Полная энергия
- •25.Работа и мощность силы
- •26. Закон сохранения импульса. Следствие
- •27. Закон сохранения момента импульса. Следствия
- •28. Закон сохранения энергии. Следствия
- •29. Основной закон динамики поступательного движения
- •32. Гравитационное взаимодействие
- •33. Электромагнитное взаимодействие
- •№42 Напряжённость электрического поля
- •Поток вектора напряженности электростатического поля
- •54. Основные уравнения электромагнетизма – уравнение Максвелла
- •Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
1.Cистемы отсчёта. Инерциальные системы отсчёта
Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.
При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта.
2. Время. «Часы». Свойства часов.
Современные единицы измерения времени основаны на периодах обращения Земли вокруг своей оси и вокруг Солнца, а также обращения Луны вокруг Земли.
3. Пространство. «Линейка». Свойства линеек
Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине).
4. Скалярная и векторная формы уравнения движения
Уравне́ние движе́ния (уравнения движения) — уравнение или система уравнений, задающие закон эволюции механической или сходной динамической системы (например, поля) во времени. В уравнения движения динамической системы входит полный набор переменных, определяющий состояние этой системы (например, все координаты и скорости, или все координаты и импульсы), а также их производные по времени, что позволяет, зная такой набор в некий момент времени, вычислить его для момента времени, отстоящего на малый (бесконечно малый) промежуток времени.
5. Модели материальной точки и твердого тела. Степени свободы
Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки.
Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи.
Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Также для твёрдого тела выделяют плоское движение.
Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы.
6. Поступательное движение. Вектор линейного перемещения точки
Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению. При поступательном движении тела траектории его точек могут быть любыми кривыми линиями. При поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
7. Вращательное движение. Вектор углового перемещения
Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными. При вращательном движении все точки, принадлежащие оси вращения, будут неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.
8. Линейная скорость
v=dS/dt
9. Угловая скорость
ω=dϕ/dt
10. Линейное ускорение
a=dv/dt
11. Угловое ускорение
ε=dω/dt
12. Тангенциальное, нормальное, полное ускорение
Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением aT=Δv/Δt. Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением an=v2/r. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения a=√aT2+an2
13. Инертность тел. Масса и ее свойства.
Ма́сса — скалярная физическая величина, одна из важнейших величин в физике. Инертная масса характеризует инертность тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.
14. Импульс. Свойства импульса
И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела.
15. Центр инерции. Полный импульс
Центр инреции (центр масс)-геометрическая точка, характеризующая движение тела или системы частиц как целого.
В классической HYPERLINK "http://ru.wikipedia.org/wiki/%D0%9A%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BC%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0"механике полным импульсом системы матHYPERLINK "http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D1%87%D0%BA%D0%B0"ериальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости: p=∑I mivi
16. Момент инерции. Свойства. Теорема Штейнера
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле.
Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями: J=Jc+md2
17. Осевой момент импульса. Свойства
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: Ja=∑i=1n miri2
18. Орбитальный момент импульса. Свойства
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
19. Главные оси инерции. Свободные оси
Оси вращения, которые в отсутствие внешних сил сохраняют неизменными своё направление в пространстве, называются свободными осями вращения тела. Свободные оси вращения, конечно, являются осями симметрии. Каждое тело произвольной формы имеет три взаимно перпендикулярные оси, проходящие через центр масс (центр инерции тела), которые могут служить свободными осями вращения. Эти оси называются главными осями инерции.
20. Кинетическая энергия поступательного и вращательного движения
Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.
Основные кинематические характеристики вращательного движения тела — его угловая скорость (ω) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z: Kz=Izω и кинетическая энергия T=(1/2)Izω2.
Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки VK=VC TПОСТ=(1/2)(∑mk)Vc2 или TПОСТ=(1/2)MVC2. Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс.
21. Потенциальная энергия
Потенциальная энергия ![]() — скалярная физическая
величина,
характеризующая
способность некого тела (или материальной
точки) совершать работу за
счет своего нахождения в поле действия
сил.
— скалярная физическая
величина,
характеризующая
способность некого тела (или материальной
точки) совершать работу за
счет своего нахождения в поле действия
сил.
Единицей измерения энергии в СИ является Джоуль.
Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.
Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.
Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.
Потенциальная
энергия ![]() в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
![]() где
где ![]() — масса тела,
— масса тела, ![]() — ускорение
свободного падения,
— ускорение
свободного падения, ![]() —
высота
положения центра
масс тела
над произвольно выбранным нулевым
уровнем.
—
высота
положения центра
масс тела
над произвольно выбранным нулевым
уровнем.
22. Внутренняя энергия. Полная энергия
Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
![]()
где
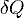 —
подведённое
к телу количество теплоты, измеренное
в джоулях
—
подведённое
к телу количество теплоты, измеренное
в джоулях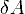 [1] — работа,
совершаемая
телом против внешних сил, измеренная
в джоулях
[1] — работа,
совершаемая
телом против внешних сил, измеренная
в джоулях
23.Силы в механике. Свойства
Мерой взаимодействия тел является сила - векторная физикеская величина.
Свойства силы:
Сила является функцией скорости и положения материальной точки.
F= f((Vx;Vy;Vz), x, y, z).
Установление этой зависимости в каждом конкретном случае является одной из основных задач в механике.
Сила, с которой одна частица действует на другую зависит от R векторов и скоростей только этих двух частиц, присутствие других частиц на эту силу не влияет. Это свойство силы называют принципом парности взаимодействия. Следствие из него называется принципом суперпозиции. .
Fрез = F1+F2+F3+...+Fn.
24.Момент силы. Свойство
Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Свойства: 1)Момент силы относительно оси не зависит от выбора плоскости на которую проектируется сила 2) Если сила параллельна оси то момент силы относительно оси равен 0. 3) если сила пересекает ось то момент силы относ. оси равен 0. 4)Если сила лежит в плоскости перпендикулярна оси то её алгебраический момент относ. точки пересечения оси с плоскостью равен моменту силы относительно.
