11. Построить метод Монте-Карло для вычисления определенного интеграла и оценить необходимое количество испытаний

Теория: , замена : , ~

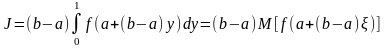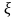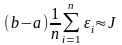
Утверждение (на семинаре): Если с.в. с , тогда D[g(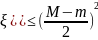

Задача (на семинаре): Вычислить приближенно интеграл с точностью с

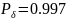
Решение: замена x=a+(b-a)y=0+(2-0)y=2y => ,

Доверительный интервал строим по принципу асимптотической нормальности

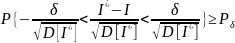, при этом достаточно для выч-ния нер-ва

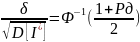
=> (Ограничение по утверждению)

12. Построить метод Монте-Карло для вычисления несобственного интеграла (приведением к плотности вероятности нормального или показательного распределения) и оценить необходимое число испытаний.

Теория:

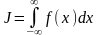
В некоторых случаях удается ввести такую функцию плотности вероятности 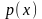, что: , и сходится .

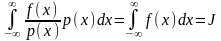, задача приближенного вычисления сводится к задаче приближенного вычисления математического ожидания , где случайная величина имеет функцию плотности вероятности .

.

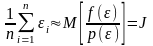Задача (семинар):

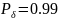, свести к показательному распределению

Решение:

,