
- •1. Задана выборка, требуется найти информацию Фишера.
- •3. Задана выбора, требуется построить оценку указанным методом (дополнительно выяснить свойства оценки: несмещенность, состоятельность и эффективность).
- •4. Задано наблюдение (не обязательно выборка) построить доверительный интервал.
- •5. Построить критерий хи-квадрат для проверки простой гипотезы о вероятностях.
- •6. Построить критерий хи-квадрат для проверки гипотезы о независимости признаков.
- •8. Задана выборка, построить наиболее мощный критерий (критерий Неймана-Пирсона) в задаче различения двух простых гипотез.
- •9. Задана выборка, построить «приближенный» критерий отношения вероятностей в задаче различения двух простых гипотез.
- •10. Построить метод Монте-Карло для вычисления функции распределения и оценить необходимое число испытаний.
- •11. Построить метод Монте-Карло для вычисления определенного интеграла и оценить необходимое количество испытаний
- •12. Построить метод Монте-Карло для вычисления несобственного интеграла (приведением к плотности вероятности нормального или показательного распределения) и оценить необходимое число испытаний.
8. Задана выборка, построить наиболее мощный критерий (критерий Неймана-Пирсона) в задаче различения двух простых гипотез.
Алгоритм:
1) Определить
плотности вероятностей для гипотез
и

2) Составим
область Г1 , такую что :
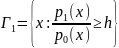
2.1) Взять ln от правой и левой частей неравенства.
2.2) Привести
неравенство к виду :
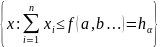
При
 принимается
,
иначе принимается
.
принимается
,
иначе принимается
.
3)Определить параметры распределения с.в. либо из условия задачи, либо через плотность распределения:

4)

5) Исходя из системы
 находим n и
определяем значение порога
находим n и
определяем значение порога

Пример
Пусть – выборка из распределения Лапласа

Построить
критерий Неймона-Пирсона для заданных
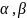 .
.
Решение
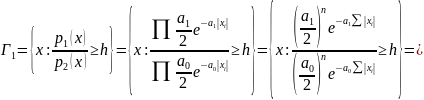
При
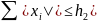 принимается
,
иначе
.
принимается
,
иначе
.

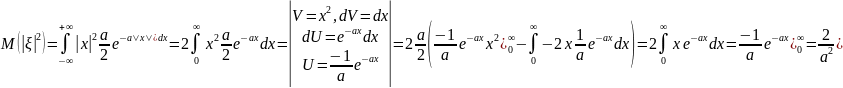


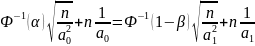 Тогда
Тогда
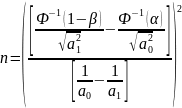 .
.
9. Задана выборка, построить «приближенный» критерий отношения вероятностей в задаче различения двух простых гипотез.
Алгоритм:
1. Записать
отношение правдоподобия в виде
 ,
где
,
где
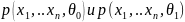 – плотности вероятностей.
– плотности вероятностей.
2. Составляем неравенство:

3. Приведем
к виду:
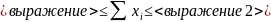
4. Записываем формулу среднего числа наблюдений для
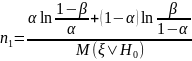
Вычисляем
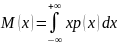 при
при
Вычисляем

Находим
значение
 ,
подставив в него
,
подставив в него
 .
.
Подставляем
в формулу для
 .
.
5. Записываем формулу среднего числа наблюдений для
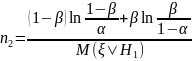
Аналогично
находим
 в формулу для
в формулу для
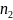 .
.
Пример:
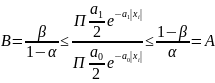
А и В
поменяны местами, т.к.
 – убывает.
– убывает.

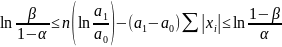
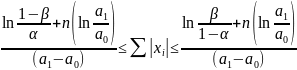
(1)
При
:
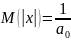 ,
,
 подставим
в (1).
подставим
в (1).
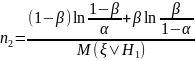 (2)
(2)
При
:
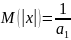 ,
,
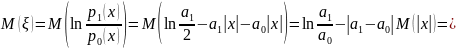
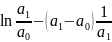 подставим
в (2).
подставим
в (2).


10. Построить метод Монте-Карло для вычисления функции распределения и оценить необходимое число испытаний.
Теория:
идея метода Монте-Карло:
подбирается случайная величина
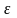 такая, что
такая, что
 и известен метод получения величины
;
и известен метод получения величины
;производится -кратное получение величины , результатом которого является вектор величин
 ,
в котором все величины
,
в котором все величины
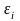 имеют такое же распределение как и
величина
;
имеют такое же распределение как и
величина
;вычисляется величина
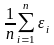 ,
которая используется в качестве
приближенного значения
,
которая используется в качестве
приближенного значения
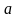 .
.
Обычно
в задачах предполагают, что умеют
получать независимые реализации
случайной величины (например
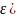 ,
равномерно распределенной на отрезке.
,
равномерно распределенной на отрезке.
Метод
получения случайных величин с
распределением
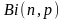 .
.
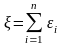 ,
где
,
где

Метод
получения случайных величин с
распределением
 .
.
Пусть
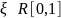 ,
тогда
,
тогда
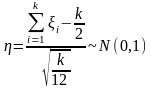 ,
,
Для
:
 ,
,
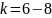
Метод получения случайной величины с заданной функцией распределения.
Пусть
,
требуется
получить случайную величину непрерывного
типа с функцией распределения
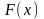 ,
имеющей обратную функцию
,
имеющей обратную функцию
 ,
образуем случайную величину
,
образуем случайную величину
 :
:
 .
.
Функция
распределения
есть функция
.
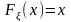 ,
,
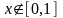 .
.
Например, для показательного распределения: получить случайную величину
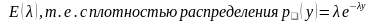 .
Ее функция распределения
.
Ее функция распределения
x=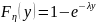 ,
а обратная функция к
,
а обратная функция к
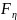 :
:

Тогда
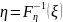 =
=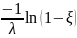
Определения
числа испытаний n
для
достижения точности
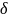
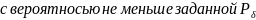 :
:
Пусть
в задаче приближенного вычисления
неизвестной величины
по методу Монте-Карло со случайной
величиной
(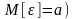 и вектором независимых случайных величин
ставится дополнительное условие о том,
что вычисленное значение должно
отличаться от
на малую величину
и вектором независимых случайных величин
ставится дополнительное условие о том,
что вычисленное значение должно
отличаться от
на малую величину
 с вероятностью не меньше заданной
с вероятностью не меньше заданной
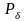 (близкой к 1). Каким образом следует
выбирать число
суммируемых величин для удовлетворения
дополнительного условия?
(близкой к 1). Каким образом следует
выбирать число
суммируемых величин для удовлетворения
дополнительного условия?
Формально дополнительное условие имеет вид:
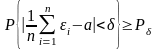 .
.
Для оценки количества требуется вычислить вероятность в левой части неравенства, и для вычисления в некоторых случаях допустимо использовать независимость величин и асимптотическую нормальность суммы:
 при
,
при
,
Получаем,
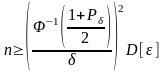
Задача (на семинаре): Определить функцию распределения случайной величины
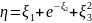 ,
где
,
где
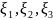 -
независимы,
-
независимы,
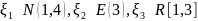
Построить
вычислительный процесс и определить
число n,
достаточное для достижения точности
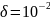 с
с
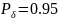
Решение:
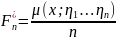 ->
строим выборку
->
строим выборку
Будем
считать, что имеется способ построения
реализаций независимых случайных
величин
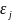 R[0,1]
R[0,1]
Образуем
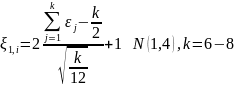
Функция
распределения
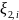 :
:
 .
Необходимо найти обратную функцию
.
Необходимо найти обратную функцию
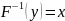 :
:
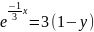 =>
=>
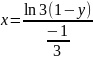 =>
=>

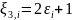
Необходимо
k
штук случайных величин
 для
нахождения
для
нахождения
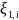 ,
(k+1)-я
- для
,
(к+2)-я для
,
(k+1)-я
- для
,
(к+2)-я для

Теперь
найдем число n,
достаточное для достижения точности
с
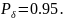
Из
условия:
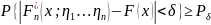
 (неравенство
Чебышева)
(неравенство
Чебышева)
отсюда
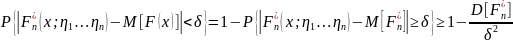
Очевидно,
что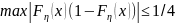 и
и
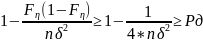
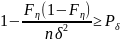 =>
(1-
=>
(1-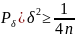 => n
=> n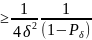
n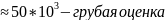 для Pд=0,95,
для Pд=0,95,

