6. Построить критерий хи-квадрат для проверки гипотезы о независимости признаков.

Теория: проводится независимых испытаний, в каждом из которых происходит в точности одно из событий , …, и в точности одно из событий , …, , вероятности совместного наступления событий неизвестны. Фиксируется количество наступлений каждой пары , наблюдение имеет полиномиальное распределение .

заключается в том, что события и попарно независимы, то есть , или иначе неизвестные вероятности при некоторых числах и , где вектор вероятностей играет роль параметра: : , , .

Используется критерий хи-квадрат проверки сложной гипотезы со статистикой,

,

где вектор вероятностей является МП-оценкой и , .

Таким образом, статистика 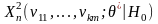имеет вид:

,

, .

Распределение статистики 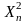стремится при к распределению .

В качестве критической области выбирается область вида:

где – квантиль уровня распределения и – заданный уровень значимости.

Задача:

Действие лекарства зависит, от способа применения:

Результат Способ	1	2	3
Нет 0	11	17	16
Есть 1	20	23	19

Проверить гипотезу о независимости результатов и способов.

Решение: ; ,

,

;

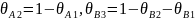
События A₁ – нет результата, А₂ – есть результат B_i – i-ый способ.

(вместо n брали (k-1)(m-1)=(2-1)(3-1)=2) и по таблице определили => гипотезу принимаем

7. Построить критерий хи-квадрат для проверки гипотезы об однородности.

А теперь забудем формулу, которая была в лекциях, ЗАБУДЕМ и всё.

Нам пригодится вот ЭТО, где

Если гипотеза Н верна, то по теореме Фишера асимптотически распределена по закону хи-квадрат с числом степеней свободы

и потому, если , то гипотезу о независимости признаков следует отклонить.

Теперь пример

У людей брали кровь. Требуется проверить гипотезу об однородности для групп крови:

Группа крови/набор	I	II	III	IV
А	121	120	79	33
B	118	95	121	30

Образуем новую таблицу

Группа крови/набор	I	II	III	IV
А	121	120	79	33	121+120+73+33=353
B	118	95	121	30	229+95+121+30=364
	121+118=239	120+95=215	79+121=200	33+30=63	сумма=717

Теперь подставляем в формулу для Хи-квадрат (банальное возведение в квадрат ячейки и деление на соответствующие строку и столбец суммарных частот):

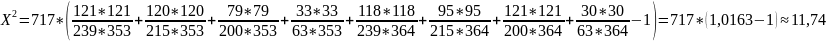
Смотрим табличку, чтобы получить наше α (1-cummulative p в Статистике)

Данная вероятность мала, критерий отклоняет гипотезу