1. Задана выборка, требуется найти информацию Фишера.
Теория:
Опр.
Пусть
– вектор случайных величин и
– функция вклада. Функция
называется
информацией
Фишера
о параметре
,
содержащейся в наблюдении
.
Формулы:
1.
2.
3.
,
где
информация Фишера, содержащаяся в
наблюдении, образованном одной случайной
величиной
.
4.
В случае выборки:
-информация,
содержащаяся
в наблюдении, образованном любой
случайной величиной
.
Задача:
а)
;
;
б)
в) E(
;
;
г)
;
;
;
д) Бинарная
:
–
n испытаний
2. Задана выборка,
требуется найти достаточную статистику
(многомерную).
-достаточная
для
,
если
(x)=h(x)
g(T,
,
т.е. надо искать
,
при которой плотность распределения
(x)
будет иметь такой вид.
Бернулли (т. величин) Т=
- достаточная
(
-
достаточная статистикa
по критерию факторизации
для
,
)
- достаточная
E(a)
-
достаточная статистикa
3. Задана выбора, требуется построить оценку указанным методом (дополнительно выяснить свойства оценки: несмещенность, состоятельность и эффективность).
Методы: МП, моменты, порядковые статистики
Теория:
Определение 1.
Оценка
является
несмещенной оценкой
,
если
:
,
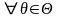где
)
и
функция распределения выборки
.
Определение 2.
Оценка
называется состоятельной, если при
каждом
:
при
.
Определение 3.
Оценка
называется эффективной оценкой
,
если
1)
является несмещенной оценкой
:
,
2) дисперсия
оценки
совпадает с нижней границей Рао-Крамера:
.
Теорема(неравенство Рао-Крамера)
Пусть
наблюдение представляет собой вектор
случайных величин
,
– функция правдоподобия вектора
,
параметр
,
где
– непустое множество допустимых значений
параметра,
– оценка величины
.
Если,
1) статистика является несмещенной оценкой величины ;
2) функция дифференцируема по при всех ;
3) выполнены условия регулярности R1-R5;
4) при всех существует производная:
;
Тогда
,
где
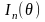информация Фишера о параметре
,
содержащаяся в наблюдении
.
А) Метод моментов
Ищем выборочный момент или центральный момент, выражаем из него параметр .
Выписываем оценку для момента (как
правило достаточно знать
)
Задача 1
– выборка из Е(а), а – неизвестно.
Построить оценки неизвестного параметра следующими методами моментов, максимального правдоподобия, порядковой статистики.
Решение
то
медиана
Задача 2
(
)-выборка
из R[a,b]
Построить оценку параметра (a,b) методом а)моментов
Решение
R[a,b]
Ответ:
,
где
Б) Метод порядковых статистик
Задача 1
– выборка из N(m,σ2). Построить оценку (m,σ2) методом порядковых статистик.
Решение
a)
медиана
б)
- функции распределения
Ответ:
В) Метод максимального правдоподобия
Задача 1
( )-выборка из R[a,b]
Построить оценку параметра (a,b) методом максимального правдоподобия
Решение
Функция правдоподобия
Ответ: