19. Дослідження функцій : достатні умови опуклості та увігнутості функції ,точки перегину,

Достатня умова опуклості та вгнутості графіка на проміжку

Теорема 3.14. Якщо функція   має неперервну другу похідну на проміжку Х, то за умови   ( )   графік  опуклий (угнутий).

 

Доведення. Візьмемо на графіку довільну точку  .

Рис. 3.13

Доведемо, що за умови   всі точки графіка будуть розміщені під дотичною, тобто, що різниця   ординати графіка   і ординати дотичної   на проміжку Х буде від’ємною:   (рис. 3.13). Складемо рівняння дотичної   в точці  : .

 

Розглянемо різницю:  . За теоремою Лагранжа для різниці   матимемо:

 

.

Тоді

 

Ще раз застосуємо теорему Лагранжа для різниці  , матимемо

.

Оскільки   і  , а  , то  , тобто, точки графіка розміщені під дотичною.

Аналогічно доводиться достатня умова вгнутості графіка на проміжку.

 

Точки перегину

Означення 3.9. Точка, яка відокремлює опуклу частину неперервної кривої   від угнутої, називається точкою перегину (inflection point).

На рис. 3.14 точка   є точкою перегину.

 

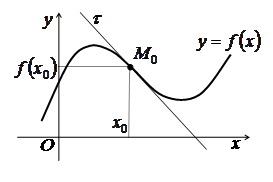
Рис. 3.14

Теорема 3.15 (необхідна умова точки перегину). Якщо точка   є точкою перегину графіка функції  , то друга похідна функції   в точці   дорівнює нулю або не існує.

Доведення. Оскільки точка   є точкою перегину графіка функції, то зліва і справа від точки   друга похідна має різні знаки. Отже, в самій цій точці друга похідна дорівнює нулю або не існує.

 

Означення 3.10. Внутрішні точки області визначення функції, в яких друга похідна дорівнює нулю або не існує, називаються критичними точками другого роду.

Попередня теорема дає всі підстави стверджувати, що точки перегину можуть знаходитись лише серед множини критичних точок.

Теорема 3.16 (достатня умова точки перегину). Нехай в точці   друга похідна функції   дорівнює нулю або не існує. Якщо при переході значень x через точку   друга похідна змінює знак, то точка графіка з абсцисою   є точкою перегину.

Доведення. Нехай при  , а при  , тоді зліва від точки   крива – опукла, а справа – угнута. Це означає, що точка   є точкою перегину.

 

Схема дослідження функції на проміжки вгнутості та опуклості

1.     З’ясовують область визначення заданої функції  .

2.     Шукають другу похідну функції  .

3.     Прирівнюють другу похідну до нуля і знаходять корені рівняння   та точки, в яких похідна не існує.

4.     Наносять одержані розв’язки рівняння   (зафарбовані точки) та точки, в яких похідна не існує («виколоті» точки), на числову вісь. Ці точки розбивають числову вісь на числові проміжки.

5.     Досліджують знак другої похідної на кожному числовому проміжку. З цією метою з кожного проміжку вибирають довільне значення (точку) та з’ясовують знак другої похідної в цій точці.

6.     За одержаними результатами формуємо відповідь.

Асимптоти графіка функції (asymptote to graph of function curve)

Означення 3.11. Пряма   називається похилою асимптотою (sloping asymptote) графіка функції  , якщо при   ( ) справедлива рівність

,                            (3.23)

 

де   при   ( ).

 

Геометрично (рис. 3.15) рівність (3.23) означає, що графік   як завгодно близько наближається до графіка   при   ( )

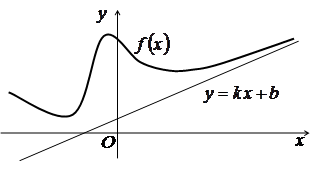
Рис. 3.15

 

З означення 3.11 (формула (3.23)) випливає, що невідомі коефіцієнти k і b в рівнянні   можна знайти так (розглянемо випадок  ):

,                                    (3.24)

.                                 (3.25)

 

Формули, аналогічні (3.24), (3.25), мають місце і у випадку  .

 

Приклад 3.38. Знайти похилу асимптоту для функції  .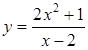

Розв’язання. Рівняння асимптоти шукатимемо у вигляді  . Знаходимо невідомі коефіцієнти за формулами (3.24), (3.25)

,

 

.

 

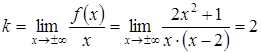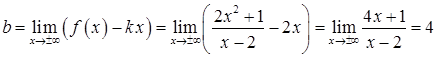Отже, пряма   є похилою асимптотою як при  , так і при  .

 

Означення 3.12. Пряма   називається вертикальною асимптотою (vertical asymptote) графіка функції  , якщо справедлива хоча б одна рівність

 

 або  .

 

Відмітимо, що пряма   є вертикальною асимптотою для функції   тоді і тільки тоді, коли точка   є точкою розриву другого роду (випадок, коли хоча б одна з односторонніх границь нескінченна) для функції  .

Отже, задача знаходження вертикальних асимптот еквівалентна задачі відшукання точок розриву другого роду типу „нескінченний стрибок” (infinite discontinuity).

 

Приклад 3.39. Знайти вертикальні асимптоти функції  .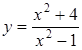

 

Розв’язання. Областю визначення даної функції є множина всіх дійсних чисел, за винятком точок   і  . Отже, точками розриву можуть бути лише ці дві точки. Досліджуючи на розрив, впевнюємось, що   і   - точки розриву другого роду типу „нескінченний стрибок”.

Отже прямі   і   - вертикальні асимптоти.

20. Загальна схема дослідження функції та побудова її графіка Загальна схема дослідження функції

 

Наведемо схему, за якою доцільно досліджувати графік функції.

1) Знайти область визначення, перевірити функцію на парність, непарність, періодичність.

2) Визначити область неперервності та точки розриву.

3) Знайти асимптоти графіка функції.

4) Знайти критичні точки першого роду, визначити проміжки зростання і спадання функції, знайти точки локального екстремуму.

5) Знайти точки перегину, проміжки опуклості і вгнутості.

6) Знайти точки перетину графіка з віссю ординат; точки перетину з віссю абсцис (якщо це можливо); інші контрольні точки.

7) За одержаними результатами побудувати  ескіз графіка функції.

1. Поняття первісної функції та її властивості.

Означення. Функція F(x) на заданому проміжку називається первісною для функції f(x), для всіх xз цього проміжку, якщо F'(x)=f(x).

Операція знаходження первісної для функції називається інтегруванням. Вона є оберненою до операції диференціювання.

Теорема. Всяка неперервна на проміжку функція (x) має первісну на цьому проміжку.

Теорема (основна властивість первісної). Якщо на деякому проміжку функція F(x) є первісною для функції f(x), то на цьому проміжку первісною для f(x) буде також функція F(x)+C, де Cдовільна стала.

З цієї теореми випливає, що коли f(x) має на заданому проміжку первісну функцію F(x), то цих первісних безліч. Надаючи C довільних числових значень, кожного разу діставатимемо первісну функцію.

2. Невизначений інтеграл: означення та елементарні властивості .Таблиця основних інтегралів.

Поняття невизначеного інтегралу

Означення. Множина всіх первісних функцій для функції f(x) називається невизначеним інтегралом і позначається  .

При цьому f(x) називається підінтегральною функцією, а f(x)dx - підінтегральним виразом.

Отже, якщо F(x), є первісною для f(x), то  .

Властивості невизначеного інтегралу

.
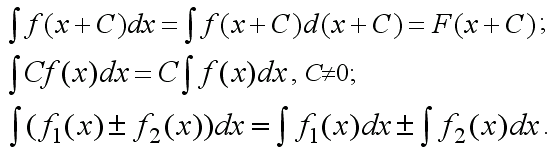
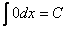2.   .
3.   .
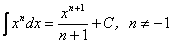4.   .
5.
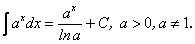
6.
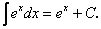
7.   .
8.
9.   .
10.  .
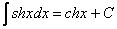11.  .
12.  .
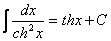13.  .
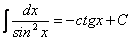14.  .
15.
16.
17.
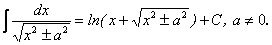
18.
19.  .
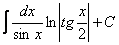20.  .
21.  .
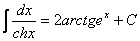22.  .
23.

3. Методи безпосереднього інтегрування та інтегрування частинами .Приклади.

Метод безпосереднього інтегрування

Цей метод базується на рівності  сталі і застосовується у тих випадках, коли підінтегрільна функція f має вигляд однієї із підінтегральних функцій таб­личних інтегралів, але її аргумент відрізняється від змінної інтегрування постійном доданком або постійним множником або постійним множником та постійним доданком.

Приклад. Знайти інтеграли

а)  b)   с) 

Розв’язування.

а)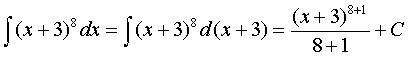 

У цьому випадку змінна інтегрування х відрізняється від аргумента степеневої функції u8 = (ч + 3)8 на постійний доданок 3;

Метод інтегрування частинами

Докладніше: Інтегрування частинами

Цей метод застосовується тоді, коли під інтегралом є добуток функцій, причому хоча би одна з них є трансцендентною (не степеневою).

Нехай u та v деякі функції х, тобто  .

Розглянемо диференціал добутку цих функцій.

Інтегруючи обидві частини рівності, одержимо 

Звідси, враховуючи властивість невизначеного інтеграла, маємо

Отже, одержали формулу 

яку називають формулою інтегрування частинами.

Ця формула дозволяє знаходження інтеграла   звести до зна­ходження інтеграла  . При вдалому обранні u то dv інтеграл може бути табличним або простішим ніж заданий інтеграл 

Приклад. Знайти 

Розв'язування. Нехай u = lnx, dv = dx. Тоді v = x

За формулою інтегрування частинами одержимо