2) Закон Кулона.

Если размерами заряженного тела можно пренебречь по сравнению с расстояниями до других тел, то такое тело называется точечным зарядом. Закон Кулона гласит, что сила взаимодействия двух неподвижных точечных зарядов, находящихся в вакууме, пропорциональна величинам зарядов q1 и q2 и обратно пропорциональна квадрату расстояния r между ними:

K – коэффициент пропорциональности. Направлена сила вдоль соединяющей заряды прямой. Экспериментально установлено, что сила взаимодействия двух зарядов не изменяется, если вблизи них поместить еще какие-либо заряды. Вместо коэффициента пропорциональности часто используют коэффициент, называемый электрической постоянной. Отсюда следует: . Тогда закон Кулона выглядит следующим образом: .

3) Напряженность электростатического поля. Принцип суперпозиции электрических полей. Вектор напряженности. Силовые линии.

Взаимодействие подвижных зарядов осуществляется посредством электрического поля. В качестве величины, характеризующей электрическое поле в точке, выступает вектор напряженности. 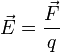. Это определение распространяется на все поля, создаваемые любой совокупностью неподвижных зарядов. Расположение зарядов, возбуждающих исследуемое поле, может измениться под воздействием пробного заряда, поэтому, чтобы не внести заметных изменений в поле, пробный заряд должен быть достаточно малым. Направление вектора совпадает с направлением силы, действующей на положительный заряд. Размерность вольт на метр. Согласно формуле на точечный заряд в точке поля с напряженностью Е действует сила F=qЕ. Если q>0, направление силы совпадает с направлением вектора Е; если q<0, направление векторов F и Е противоположны. Напряженность поля системы зарядов равна векторной сумме напряженностей поле, которые создавал бы каждый из зарядов в отдельности Е=ΣЕi . Поля складываются, не возмущая друг друга. Это утверждение носит название принципа суперпозиции. Принцип суперпозиции позволяет вычислить напряженность поля любой системы зарядов. Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля. Силовые линии проводятся с такой густотой, чтобы число линий, пронизывающих воображаемую площадку 1м2, перпендикулярную полю, равнялось величине напряженности поля в данном месте. Тогда по изображению электрического поля можно судить не только о направлении, но и о величине напряженности поля. Электрическое поле называется однородным, если во всех его точках напряженность Е одинакова. В противном случае поле называется неоднородным.

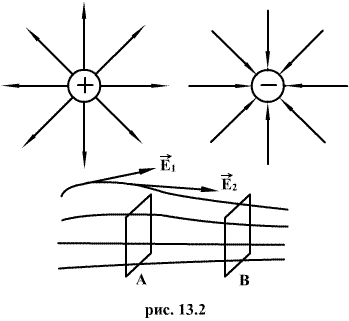
4)Поток вектора напряженности. Закон Гаусса в интегральной форме.

Поток вектора напряженности электрического поля через произвольную поверхность численно равен количеству линий напряженности, пронизывающих эту поверхность.

Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).

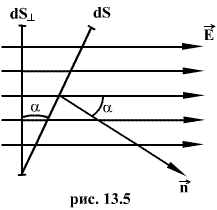
Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5). , где   - угол между силовой линией и нормалью   к площадке dS;   - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен , где   - проекция вектора   на нормаль и к поверхности dS. Теорема Гаусса: поток вектора напряженности электростатического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на  .  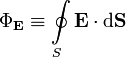= (1/ )Σq. 5)Работа электрического поля точечного заряда.