34. Взаимное расположение плоскостей.
Взаимное расположение плоскостей в пространстве: плоскости в пространстве могут быть совпадающими, пересекающимися, параллельными. Пусть
α: А1х+В1у+С1z+Д1=0;
β:
А2х+В2у+С2z+Д2=0.
Рассмотрим случаи: 1)
плоскости α и β совпадают или параллельны.
В этом случае считается, что (α^β)=00;
при этом пишут α׀׀β.
Если α׀׀β,
то
,
(в частном случае: А1=А2, В1=В2, С1=С2).
2) плоскости α и β перпендикулярны. В этом случае считают, что (α^β)=900 и пишут α⟘β. Если α⟘β, то nα*nβ=0, т.е. А1*А2+В1*В2+С1*С2=0.
35. Расстояние от точки до плоскости.
Пусть
плоскость α задается общим уравнением:
Ах+Ву+Сz=0.
Расстояние от точки F
до плоскости α обозначается ρ(F;α).
Расстояние от точки до плоскости –
наикротчайшее расстояние от этой точки
до данной плоскости. Известно, что
ρ(F;α)
есть длина перпендикуляра, опущенного
из точки F
на плоскость α. Справедлива
формула:
ρ(F;α)=
44. Кривые второго порядка на плоскости: эксцентриситет и директрисы.
Эксцентриситет
обозначается e
или E.
Считается, что 1)
для эллипса Е=с/а <1; 2)
для гиперболы Е=с/а >1; 3)
для параболы Е=1. Для эллипса и гиперболы
вводится понятие директрисы.
В этом случае директрисами являются
прямые х=
а/Е.
45. Поверхности второго порядка в пространстве.
Пусть
в пространстве задана система координат
хуzО.
Поверхностью
2го порядка
называется множество точек с координатами
(х, у, z),
координаты которых удовлетворяют ур-ю:
а11х2+а22у2+а33z2+а12ху+а13хz+а23уz+а1х+а2у+а3z=0,
где а11, а22, а12, а13, а23 одновременно не
равны нулю. К классическим поверхностям
2го порядка относятся поверхности
вращения,
цилиндры и конусы.
1)
поверхность
вращения.
Задание:
кривая, лежащая в плоскости; прямая
(ось вращения). Через точку М и ось
вращения проводится плоскость,
перпендикулярная оси вращения. В этой
плоскости точка М вращается по окружности,
центр которой расположен на оси вращения.
Таким образом поступаем с каждой точкой
данной прямой; получается поверхность,
называемая поверхностью вращения. 2)
цилиндрическая
поверхность (цилиндр).
Задание:
кривая, лежащая в плоскости; прямая
(направляющая цилиндра). Через точку М
проводим прямую, параллельную направляющей
цилиндра. Таким образом поступаем с
каждой точкой кривой и получаем
цилиндрическую поверхность. 3)коническая
поверхность (конус). Задание:
кривая, лежащая в плоскости; точка(вершина
конуса). Через точку М и вершину конуса
проводим прямую. Таким образом поступаем
с каждой точкой кривой и получаем
коническую поверхность. Также к
классическим поверхностям 2го порядка
относят эллипсоиды,
гиперболоиды, параболоиды.
1)
эллипсоид.
Данная поверхность в системе координат
хуzО
задается уравнением:
Проекциями эллипсоида на координатные
плоскости являются эллипсы. Например,
в плоскости хОу получаем эллипс
2)
гиперболоид.
а)однополостный
гиперболоид. Данная поверхность в
системе координат хуzO
задается уравнением:
.В
плоскости хОу (т.е. где z=0)
получаем эллипс
и уОz
получаем гиперболу
и
.
При пересечении поверхностей плоскости
параллельной хОу в сечении образуется
эллипс. б)
двуполостный гиперболоид. Данная
поверхность в системе координат хуzО
задается уравнением:
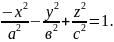В плоскости хОz
и уОz
получаем гиперболы:
и -
Заметим,
что |z|
с.
При |z|
с
в сечении поверхности с плоскостью,
параллельной плоскости хОу, получаем
эллипс. 3)
параболоиды.
а)
эллиптический параболоид. Данная
поверхность в системе координат хуzО
задается уравнением: :
Заметим, что z
c.
В сечениях поверхности плоскостям,
параллельным поверхности хОу, получаем
эллипсы. В плоскости хОz
и уОz
получаем параболу
и
.
6)
гиперболический
параболоид.
Данная поверхность в системе координат
хуzО
задается уравнением
