5. Матрица системы линейных уравнений и матрично-векторная запись слу.

Теорема Кронекера-Капелли о совместности СЛУ.

Систему из m линейных уравнений с n неизвестными

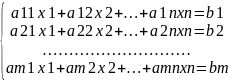
можно представить в матричном виде

A= ; X= ; B=

и тогда всю СЛУ можно записать так: АХ=В, где А имеет смысл таблицы коэффициентов а_ij  СЛУ. Если m=n  и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A^-1, поскольку умножив обе части уравнения на эту матрицу слева:

А^-1АХ=А^-1B, А^-1А – превращается в Е (единичную матрицу). И это даёт возможность получить столбец корней уравнений Х=А^-1В. Все правила, по которым проводятся операции над матрицами, выводятся из операций над системами уравнений.

Теорема Кронекера-Капелли. Пусть дана система: . Составим две матрицы: А= ; Ã= . Пусть r_А- ранг векторов-строк матрицы А, r_Ã- ранг векторов-строк матрицы Ã. Теорема: СЛУ совместна тогда и только тогда, когда r_А= r_Ã.

11. Матрицы. Размерность матрицы. Специальные матрицы (нулевая,

единичная, квадратная).

Множество действительных чисел R. Матрицей называется прямоугольная таблица чисел. Размерностью матрицы называется пара чисел, обозначаемая mхn, где m – количество строк, n – количество столбцов. Общий вид матрицы следующий: A= =(a_ij)_mxn.

Множество всех матриц размерности mxn обозначается Мmxn ( R ). Две матрицы А и В одинаковой размерности называются равными, если соответствующие элементы этих матриц равны. При этом пишут А=В.

Нулевая матрица – это матрица размерности mxn, все элементы которой равны нулю. Нулевая матрица, и только она, имеет ранг=0. Это означает, что только нулевая матрица обладает свойством давать нулевой столбец при умножении справа на любой вектор-столбец, и аналогично для умножения вектор-строки слева. Единичная матрица – квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю. Матрица, в которой количество строк совпадает с количеством столбцов называется квадратной.

12. Сложение матриц, свойства.

Сумма матриц А и В ϵ Мmxn называется матрица А+В, которая получается путем сложения соответствующих элементов матриц А и В. Свойства сложения матриц: Пусть А, В, С ϵ Мmxn. 1) А+В=В+А 2) (А+В)+С=А+(В+С) 3) А+Ѳ=А, где Ѳ-матрица, элементами которой являются нули (нулевая матрица).

13. Умножение матрицы на число, свойства.

Произведение матрицы А ϵ Мmxn на число α ϵ R, называется матрица, обозначаемая αА, которая получается путем умножения всех элементов матрицы А на число α. Свойства умножения матрицы на число: Пусть А, В ϵ Mmxn и α, β ϵ R. 1) α(βА)=(αβ)А 2) α(А+В)=αА+αВ 3) (α+β)А=αА+βА 4) 1А=А 5) 0А=Ѳ 6) αѲ=Ѳ.

14. Умножение матриц, свойства.

Пусть А ϵ Мmxn, В ϵ Мnxk. А_i - i-я строка матрицы А, В^j – j-й столбец матрицы В. Тогда А_i=(a_i1, a_i2, …, a_in), B^j=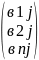 . Произведение строки А_i на столбец B^j называется число, обозначаемое A_i*B^j, которое вычисляется по формуле: A_i*B^j = a_i1в_1j+a_i2в_2j+…+a_imв_nj. Произведение матрицы А на матрицу В называется матрица, обозначаемая А*В, элементы которой равны A_i*B^j для всех i=1,2,…,n; j=1,2,3,…,k. Свойства умножения: Пусть А, В, С матрицы, α – число. 1) (АВ)С=А(ВС) 2) (αА)В=α(АВ) 3) (А+В)С=АС+ВС 4) С(А+В)=АС+ВС, НО! АВ не всегда = ВА.