11. Производные элементарных функций

1.

2.

3.

4. ,

5.

6.

7.

8.

9.

10.

11.

12.

13. ,

14. ,

15. ,

16. ,

12. Геометрический смысл производной, уравнение касательной и нормали к кривой.

П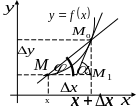 усть - фиксированная точка, - текущая, - секущая. При секущая переходит в касательную в точке (предельное положение секущей).

если то

.

Далее, нам известно уравнение прямой линии

Здесь . Отсюда

- уравнение касательной

- уравнение прямой, перпендикулярной данной.

- нормали.

Производные высших порядков явно заданных функций

Производной второго порядка, или второй производной, функции называется производная от ее производной .

Обозначение второй производной

Аналогично определяются и обозначаются производные третьего, четвертого и более высоких порядков

Производные порядка обозначаются и так

Если функция задана параметрически: , , то ее вторая производная определяется формулой

13. Дифференциал функции.

Пусть функция определена в окрестности и имеет производную в этой точке

При этом . Тогда для достаточно малых можно записать

Причем при . В этом случае приращение функции можно записать в виде

Или

Определение. Функция называется дифференцируемой в точке , если ее приращение можно представить в виде

где не зависит от , но вообще зависит от .

Теорема 9. Для того чтобы функция была дифференцируема в точке , необходимо и достаточно, чтобы она имела конечную производную в этой точке.

Таким образом, сказать, что имеет производную в точке или что дифференцируема в точке - это одно и то же. Поэтому процесс нахождения производной называют дифференцированием функции.

Доказательство.

Достаточность условия доказана выше: из существования конечной производной следовала возможность представления в виде , где можно положить .

Необходимость. Пусть функция дифференцируема в точке . Тогда, если , можно записать

Предел левой части при существует и равен :

Это означает, что существует производная .

Геометрический смысл дифференциала.

Итак, приращение функции можно представить в виде

П ервое слагаемое пропорционально , т.е. оно - линейная однородная функция от . Второе, является бесконечно малой высшего порядка малости , т.е. оно стремится к нулю быстрее, чем первое. В связи с этим первое слагаемое называется главным членом приращения (при ). Это слагаемое называют дифференциалом функции и обозначают символом . Итак, по определению

На рисунке - касательная к кривой в точке , , приращение функции соответствует приращению аргумента . При этом

Вообще говоря . Равенство выполняется только для линейной функции. В этом случае дифференциал и приращение независимой переменной равны между собой . Поэтому дифференциал произвольной функции записывают обычно так

Основные теоремы о дифференциалах, дифференциал

сложной функции

1)

2)

3)

4)

5)

6) Форма дифференциала инвариантна (неизменна).

Дифференциал функции равен произведению производной на дифференциал аргумента независимо от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

Например, дифференциал сложной функции.

Применение дифференциалов к приближенным

вычислениям

Итак

Отсюда следует, что дифференциал функции при достаточно малом может служить хорошим приближением приращения функции. В этом смысле пишут приближенное равенство

где .

Например, вычислить значение . Имеем , , .

Далее . Или . Окончательно

Дифференциалы высших порядков.

1) Если , то .

2) Если , то

Например. Дано уравнение эллипса . Найдем первую производную

Вторая производная. Имеем . Отсюда