9. Дайте определение бесконечно малой (бм) послед-и. Приведите примеры бм послед-ей, отношение которых: а) является бм послед-ью; б) не является бм послед-ью.

Послед-ь {αn} называется бм, если lim (n→∞) αn = 0.

Для любого ε > 0, сущ. N, такое, что для любого n ≥ N | αn | < ε.

а) 1/n, 1/ ^4√n – бм послед-и: ^4√n/ n = n^-3/4 – бм послед-ь

б) n/ ^4√n = n^3/4 - не бм послед-ь

10. Докажите, что произведение бм и ограниченной послед-ей является бм послед-ью.

док-во:

Пусть {Хn} – ограниченная, а {αn} – бм послед-и. Доказать, что {Xn * αn} – бм. Так как {Хn} ограниченна, то существует число А > 0 такое, что любой элемент Хn удовлетворяет неравенству | Хn | ≤ А. Возьмем любое ε > 0. Поскольку {αn} – бм, то для положительного числа ε/А существует номер N такой, что при n > N выполняется неравенство | αn | < ε/А. Тогда при n > N |Xn * αn | = |Xn| * | αn | < A * ε/A = ε. Это означает, что послед-ь {Xn * αn} – бм.

11. Докажите, что предел произведения двух функций равен произведению их пределов, если последние существуют.

Из условия lim u=a, lim v=b следует u=a+α, v= b+β.

Рассмотрим u×v=( a+α)(b+β)=ab+bα+aβ +αβ → u×v=ab+µ → lim u×v=a×b

12. Дайте определение бесконечно большой (бб) послед-и. Что означает запись «lim (n→∞) Xn = +∞»? Докажите, исходя из определения, что lim (n→∞) √n + 9 = +∞.

1) Послед-ь {Xn} называется бб, если для любого положительного числа А существует номер N такой, что при n > N выполняется неравенство |Xn| > A. (lim (n→∞) Xn = ∞ ).

Для любого A > 0, сущ. N, для любого n ≥ N: |Xn| > A.

2) Если, начиная с некоторого номера, все Xn > 0, то lim (n→∞) Xn = +∞ (Xn > A).

3) √n + 9 > A => √n + 9 > 0 => lim (n→∞) √n + 9 = +∞; N = [A² - 9] + 1.

13. Всякая ли неограниченная послед-ь является бесконечно большой? Ответ обоснуйте.

Любая бб послед-ь является неограниченной. Однако неограниченная послед-ь может и не быть бб послед-ью. Например, неограниченная послед-ь 1, 2, 1, 3 .., 1, n, 1, n + 1 … не является бб, поскольку при А > 1 неравенство |Xn| > A не имеет места для всех элементов Xn с нечетными номерами.

14. Дайте определение предела функции в точке. Найдите, исходя из определения , lim (x→1) (7x + 3)/x² + 7. Приведите пример функции, не имеющей предела в точке x = 1.

1) Число а называется пределом функции f (x) в точке X0 (или пределом при X→ X0) если для любой сходящейся к точке X0 послед-и значений аргумента, отличных от X0, соответствующая послед-ь значений функции сходится к числу а, т. е.

lim Xn = X0 (Xn ≠ X0) => lim f(Xn) = a; lim (X→ X0) f(x) = a.

2) lim (x→1) (7x + 3)/x² + 7 = 5/4

3) y = x/x - 1 – функция, не имеющая предела в точке X = 1 (уходит в разные стороны, дробно-линейная функция).

15. Докажите, что предел суммы двух функций равен сумме их пределов, если последние существуют.

(не совсем с функциями связано, но то же свойство, вроде, может подойдет, что-то другого ничего нету)

Пусть a и b – соответственно пределы {Xn} и {Yn}. Тогда Xn = a + αn, Yn = b + βn, где {αn} и {βn} – бм послед-и. Следовательно, (Xn±Yn) – (a±b) = αn ± βn.

Послед-ь {αn ± βn} – бм. Таким образом, послед-ь {(Xn±Yn) – (a±b)} также бм и поэтому послед-ь (Xn±Yn) сходится и имеет своим пределом число a±b.

16. Докажите, что функция f(x) = sin 1/x не имеет предела в точке x = 0.

lim (x→0) sin 1/x по Гейне lim (n→∞) Xn = X0, lim(x→0+0) 1/x = +∞, lim(x→0-0) 1/x = - ∞

lim (x→0+0) sin 1/x – не сущ. sin (x→0-0) 1/x – не сущ.

17. Может ли функция f(x) +g(x) быть непрерывной в точке х0, если функция f(x) непрерывна, а функция g(x) имеет разрыв в этой точке, а функция g(x)имеет разрыв в этой точке. ответ обоснуйте.

Нет. Так как есть теорема, в которой говорится. Если f(x) и g(x)- непрерывные функции в точке x0, то непрерывными являются .

.f(x)=c-является непрерывной и f(x)=x.

18 Найдите значение а, при котором функция f(x) = x arctg (1/x), x≠0, является непрерывной в точке x=0.

lim (x→ x0) f(x) = f(x0)

является непрерывной в точке x = 0

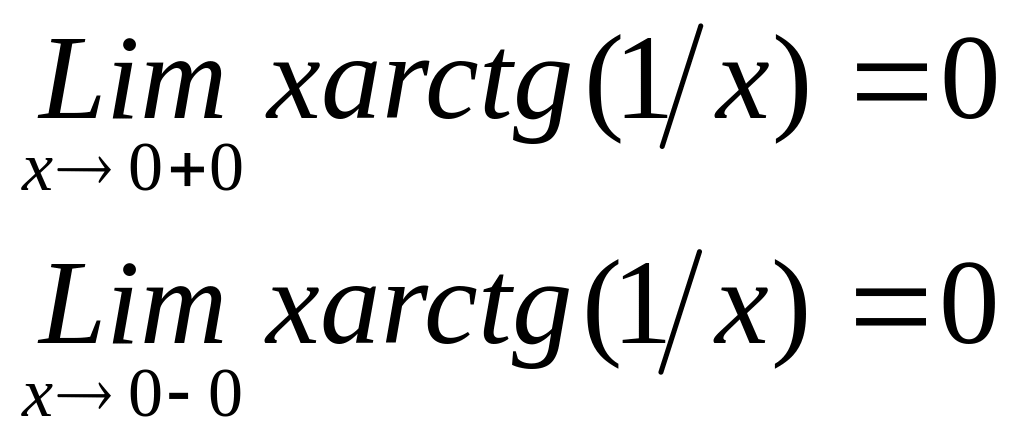следовательно

следовательно а=0

22. Функция y = f (x), определенная в некоторой окрестности точки х₀ , называется непрерывной в этой точке, если предел функции в точке х₀ существует и равен значению в этой точке: lim _{х → х0} f(x) = f(x₀).

23.Теорема о непрерывности сложной ф-ции.

Сложная функция, составленная из конечного числа суперпозиций непрерывных функций, тоже непрерывная функция.

24. Теорема о непрерывности обратной ф-ции. Функция обратная для монотонной и непрерывной функции также непрерывна.

25. Теорема о непрерывности элементарных ф-ций. Любая элементарная функция непрерывна там,где она определена.

26. Точка х₀ называется точкой разрыва функции f(x), если f(x) не являетс непрерывной в точке x0Ю то есть: , или не существует, или функция не определена в x0.

Разрыв 1 рода, если в этой точке функция имеет конечные, но не равные друг другу левый и правый (односторонние) пределы.

Разрыв 2 рода, если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов (он не существует) или хотя бы один из односторонних пределов бесконечен.

Разрыв устранимый, если функция не существует в точке х₀ или если значение функции в точке х₀ не совпадает со значением односторонних пределов.

27.определение производной в точке Пусть функция определена в некоторой окрестности точки x₀(∆x=x-x₀). (∆y=f(x)-f(x0)=f(x0+∆x)-f(x0) Производной функции в точке x₀ называется lim , когда (при условии, что lim существует). Обозначение .

28. Если функция y = f(x) имеет производную в точке х₀ , то мы говорим, что функция дифференцируема в этой точке.

29. Дифференциалом функции в точке х₀ называется линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению.

df(х₀)= f ′ (х₀) ∆х; ∆х=dх; df(х₀)= f ′ (х₀) dх

30. Общие правила дифференцирования.

( f (g (x)) )’ = f ‘(g(x)) · g ‘ (x)

(u ^v )’ = v · u ^v-1 · u’ + u^v · v’ · ln u

31.Теорема о производной обратной функции.

Если функция y=f(x) имеет обратную функцию x=g(y) и в точке х0 производная f(x) не равна нулю, то обратная функция g(y) дифференцируема в точке у0=f(x0) и g(y0)=1/f’(x0) или xy=1/yx.

32.Теорема о производной сложной функции.

.Если функция у=f(x) дифференцируема в точке t0 и g(t0)=x0, то сложная функция y=f(g(x)) также дифференцируема в t0 и выполняется следующая формула: d f(g(t))/dt|t=to=f(x0)*g(t0) или yt=yx*xt.

33. Геометрический смысл производной и дифференциала.

Приращением функции y =f(x) в точке x0 называется разность

Δу=f(x)-f(x0)= f(x+Δx)-f(x0)

Производной от функции y=f(x) в точке х0 наз. Предел отношения Δу/Δх, когда Δх→0 (при усл., что этот предел существует)

Написать обозначение производной.

Геометрический смысл производной.

Пусть Г- график функции y=f(x). Рассмотрим на Г т. А(x0,f(x0)) и т. В (x0+Δx,f(x0+Δx))

Прямая АВ называется секущей. Будем считать, что y=f(x)-непрерывная функция, тогда если Δх→0, то f(x0+Δx)→f(x0), т.е. В→А при Δх→0.

Пусть γ (от - до + пи на 2) – угол наклона секущей относительно оси ОХ. Если существует предел lim γ=γ0 при Δх→0, то прямая, проходящая через А и образующая с осью ОХ угол γ0, называется касательной к Г в точке А.

Пусть С(f(x0+Δх), f(x0)) – точка, дополняющая отрезок АВ до прямоуг. треугольника АВС. Т.к. АС//ОХ, то tgγ =Δу/Δх. Переходя к пределу, получим: tgγ0=f′(x0)

Т.е. геометрический смысл производной состоит в том, что f′(x0) – это тангенс угла наклона касательной к графику y=f(x) в точке (x0,f(x0)).

Дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции y=f(x) в данной точке, когда аргумент x получает приращение дельта x.

34. Уравнение касательной.

Найдем ур-е касательной к графику Г ф-и y=f(x) в точке А(х0, f(x0)): т.к. т. А принадлежит Г и ур-ю касательной, то f(x0)=kx0+b, откуда b= f(x0)-kx0, значит, касательная задается след. Ур-м:

y= kx+ f(x0)-kx0= f(x0)+k(х-x0)

Т.к. k= f′(x0), то

y=f(x0)+ f′(x0)(х-х0).

35. Определение эластичности функции.

Эл-ю функции y = f(x) в точке х0 называется следующий предел

Eyx(x0) = lim ((Δy/y): (Δx/x)).

Δx  0

Эластичность Ey – это коэффициент пропорциональности между относительными изменениями величин y и x.

Ey=y’/y*x=(ln y)’*x

36. Теорема Ролля.

Если функция, непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения (f(a)=f(b)), то существует точка c, принадлежащая (a, b) в которой f’(c)-0.

37. Теорема Лагранжа.

Пусть функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b). Тогда существует точка с, принадлежащая (a, b) такая, что

f(b) − f(a) = f '(c) · (b − a) .

(1)

 Формула (1) называется формулой Лагранжа, или формулой конечных приращений

38. Теорема Коши.

Пусть f(x) и g(x) определены и непрерывны на отрезке и дифференцируемы на интервале ; а также g’(x)не=0 на (a, b), тогда сущ-ет точка c принадлежащая (a, b),такая что

39. Правило Лопиталя.

Теорема (правило Лопиталя). Пусть А – число, символ одностороннего предела (А=а±0) или символ бесконечности (А=±∞). Пусть функции ƒ(х) и g(х) либо обе бесконечно малые, либо обе бесконечно большие при х→А. Тогда, если существует предел

( конечный или бесконечный),

то существует и предел

при этом выполняется равенство:

40. Производные и дифференциалы второго порядка.

Если для функции y=f(x) определена производная у(к-1) порядка (к-1), то производную у(к) порядка к (при условии ее существования) определяют как производную от производной порядка (к-1), т.е. у(к) = (у(к-1))′ . В частности, у’’=(y’)’- производная второго порядка, y’’’=(y’’)’ – третьего и т.д.

f’’(x)=(f’(x))’

Дифференциалы высших порядков ф-и y=f(x) последовательно определяются таким образом:

d²y=d(dy)=d(f'(x)dx)=(ƒ'(х)dx)'•dx=

=f"(x)dx•dx=f"(x)(dx)²

d³y=d(d²y)…

dⁿy=d(d ^n-1 y) - диф-л n-го порядка