28 Вопрос: Виды анализа данных в социологическом исследовании. Метод уточнения в анализе связи между переменными.

Методы, применяемые социологами для анализа данных, многообразны. Выбор

конкретного метода зависит:

- от характера исследовательских гипотез,

т. е. от того, на какие вопросы хотим получить ответ.:

1. Если целью является описание

одной характеристики выборки в определенный момент времени, разумно ограничиться

одномерным анализом.

2. Разнообразные техники многомерного анализа позволяют

одновременно исследовать взаимоотношения двух и более переменных и в той или иной

форме проверять гипотезы о причинных связях между ними.

• от природы полученных социологом данных. (Пример: для того чтобы охарактеризовать распределение в выборке такого

номинального признака, как «пол», мы не можем воспользоваться его

среднеарифметическим значением).

• от целей анализа и от уровня измерения исследуемых переменных. (Пример: методы, используемые для анализа связи между двумя номинальными переменными, также будут отличаться от методов анализа связи между номинальной

переменной и переменной, измеренной на интервальном уровне).

Одномерный анализ - описание распределения наблюдений («случаев») вдоль оси

интересующего нас признака.

Результаты измерения любой переменной могут быть представлены с помощью распределения наблюдений («случаев») по отдельным категориям данной переменной. Результатом упорядочения наблюдений будет их группировка. Независимо от того, какие статистические методы и модели собирается использовать исследователь, первым шагом в анализе данных всегда является построение

частотных распределений для каждой изучавшейся переменной. Полученные

результаты принято представлять в виде таблицы частотного распределения (или просто

— таблицы распределения) для каждой существенной переменной. Помимо табличного представления частотных распределений обычно используют и

различные методы графического представления (гистограмма, полигон, круговая диаграмма).

Для облегчения работы с

частотными распределениями, а также для обобщенного представления их

характеристик, обычно используют определенные статистики. Наибольшее практическое значение

имеют две группы статистик: меры центральной тенденции и меры изменчивости

(разброса).

Меры центральной тенденции указывают на расположение среднего, или типичного, значения признака, вокруг которого сгруппированы остальные наблюдения.

МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ:

1. Мода (Мо). Для номинальных переменных мода — это единственный способ указать наиболее типичное,

распространенное значение. Мода — это такое значение в совокупности наблюдений, которое встречается чаще

всего. У моды как меры центральной тенденции есть определенные недостатки, ограничивающие

ее интерпретацию:

• в распределении могут быть две и более моды (соответственно оно является бимодальным или мультимодальным).

• мода чрезвычайно чувствительна к

избранному способу группировки значений переменной.

2. Другая мера центральной тенденции — медиана — обычно используется для ординальных переменных, т. е. таких переменных, значения которых могут быть упорядочены от меньших к большим. Медиана (Md) — это значение, которое делит упорядоченное

множество данных пополам, так что одна половина наблюдений оказывается меньше

медианы, а другая — больше.

2. Среднее арифметическое, которое чаще

всего называют просто средним. Процедура определения среднего

общеизвестна: нужно просуммировать все значения наблюдений и разделить

полученную сумму на число наблюдений.

Выбирая меру центральной тенденции, нужно руководствоваться знанием ее

свойств, общей формой распределения и, наконец, здравым смыслом.

Очевидно, важно не только знать, что типично для выборки наблюдений, но и

установить, насколько выражены отклонения от типичных значений. Чтобы определить,

насколько хорошо та или иная мера центральной тенденции описывает распределение,

нужно воспользоваться какой-либо мерой изменчивости, разброса.

МЕРЫ ИЗМЕНЧИВОСТИ — это меры, позволяющие выяснить не только типичность значения, но и степень его отклонения от типичных значений:

1. Самая грубая мера изменчивости — размах (диапазон) значений. Эта мера не

учитывает индивидуальные отклонения значений, описывая лишь диапазон их

изменчивости. Под размахом понимают разность между максимальным и минимальным

наблюдаемым значением.

2. Еще одна грубая мера разброса значений — это коэффициент вариации (V), который определяется просто как процент наблюдений, лежащих вне модального

интервала, т. е. процент (доля) наблюдений, не совпадающих с модальным значением.

Если от модального отличаются 60% значений, то V = 60% (или V = 0,6).

3. Междуквартилъный размах — очень удобный показатель разброса значений для ординальной переменной. Нижний, первый, квартиль (Q1) отсекает 25%

наблюдений, а ниже третьего квартиля (Q3) лежат уже 75% случаев.

4. Полумеждуквартилъный размах (мы им и пользуемся обычно) равен половине расстояния между третьим и первым

квартилями:

Q=

Q3 − Q1

.

.

Все эти меры изменчивости, как уже говорилось, можно считать скорее грубыми и

приблизительными. А есть еще всякие финтифлюшки получше:

1. Важнейшая мера рассеяния — дисперсия (s^2). Для того чтобы вычислить значение дисперсии, нужно вычесть из каждого

наблюдаемого значения среднее, возвести в квадрат все полученные отклонения,

сложить квадраты отклонений и разделить полученную сумму на объем выборки.

Дисперсия показывает, насколько составляющие распределение величины отстоят от средней величины этого распределения. Вот:

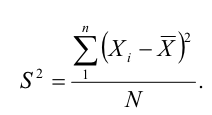
2. Стандартные отклонения

. Величина, равная квадратному корню из дисперсии, называется стандартным

отклонением (Sx). Совершенно очевидной интерпретацией стандартного отклонения является его

способность оценивать «типичность» среднего: стандартное отклонение тем меньше, чем

лучше среднее суммирует, «представляет» данную совокупность наблюдений.

Еще одно важное применение стандартного отклонения связано с тем, что оно, наряду со средним арифметическим, позволяет определить самые существенные

характеристики нормального распределения.

Описанные процедуры анализа одномерного распределения относятся к дескриптивной статистике.

Анализ связей между двумя переменными:

Большинство исследователей уделяют внимание основное анализу связей между двумя переменными. Самым простым и типичным является случай анализа взаимосвязи двух переменных. Двумерный и многомерный анализ данных позволяет проверить гипотезы о причинной зависимости двух и более переменных. Для демонстрации причинно-следственного отношения мужду двумя переменными (Х и У) необходимо выполнить три требования:

1. показать, что существует эмпирическая взаимосвязь между двумя переменными,

2. исключить возможность обратного влияния У на Х,

3. убедиться, что взаимосвязь не может быть объяснена зависимостью этих переменных от какой-то другой переменной.

Первый шаг в анализе: перекрестная классификация или построение таблицы сопряженности. Это таблица, которая содержить информацию о совместном распределении переменных.В такой таблице есть крайний столбец и крайняя строка (маргиналы таблицы) для обозначения общего количества наблюдений в данной строке или столбце.По горизонтали располагают независимую переменную, по вертикали — зависимую. Не помешает вместо абсолютных значений указать проценты.

При анализе таблицы сопряженности можно руководствоваться правилами:

1. Определить независимую переменную и пересчитать абсолютные частоты в проценты,

2. Сравнить показатели, полученные для подругпп с разным уровнем независимой переменной.

3. Есть различия? Значит, есть взаимосвязь.

Поговорим о мерах, говорящих о степени взаимосвязи.

- Основанные на хи-квадрате:

1.) Хи-квадрат.

О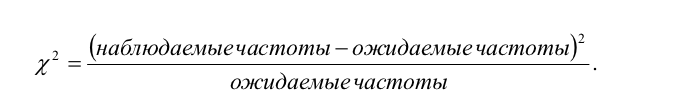 жидаемые частоты — это те, которые должны были бы стоять в клетках этой таблицы сопряженности, если бы не было взяимосвязи между переменными, если бы они были независимы.

Хи-квадрат оценивает суммарную величину отклонения наблюдаемых значений от ожидаемых. Для определения существенности полученной величины следует воспользоваться специальными таблицами. Для этого нужно знать степени свободы.

2. Коэффициент Фи. Предложен Пирсоном, чтобы сделать возможным анализ взаимосвязи между двумя переменными, измеренными на неколичественном уровне.

• Меры «пропорционального уменьшения ошибки».Они основаны на следующем предположении: если две переменные взаимосвязаны, мы можем предсказать значение одной переменной для данного наблюдения, зная, какое значение примет другая переменная.

1. В пример приведу гамма-коэффициент. Измеряет относительное уменьшение ошибки предсказания ранга конкретного наблюдения по зависимой переменной. Сначала надо упорядочить наблюдения по независимой и зависимой переменным. Потом надо сравнивать случаи попарно, определяя, сходится или расходится порядок расположения этих случаев по переменным. Если да, то пара согласованная, если нет, соответственно, несогласованная. Если согласованных пар больше, то связь велика.

Больше несогласованных — связь отрицательна. Пар одинаково? Связи нет.

Формула вот:

Многомерный анализ данных-позволяют одновременно исследовать взаимоотношения двух и более переменных и в той или иной форме проверять гипотезы о причинных связях между ними. Кросс-табуляция — таблица, где указаны как минимум 2 переменные

(н)влияние пола человека на выбор профессии а- зависимая переменная (профессия)

б- независимая (пол)

статистическая значимость различий между групп стат. Обоснов. выводы стат.анализ связей м/у 2 переменными.стадии анализа: 1)установление связей(пол влияет на профессию?) 2)измерение связи(разные коэф.пирсона,гутмана) 3)объяснение связей-причинная зависимость (н)-влияние пола на самооценку здоровья: 24м.-%, 38 %-ж, посмотреть влияние возраста

Метод уточнения — подход к анализу взаимосвязи с введением дополнительных, контрольных переменных.

Был детально разработан Лазарсфельдом , Стауффером, Кендалл для анализа элементарных таблиц сопряженности и взаимосвязей номинальных признаков.

1. Модель ложной взаимосвязи.

Чтобы произвести уточнение причинной модели, нужно понять, является ли контрольная третья переменная опосредующей или предшествующей. Если контрольная предшествует во времени независимой и зависимой, то она воздествует на них как общая причина, порождая эмпирическую взаимосвязь между ними. При это взаимосвязь не является причинной, ибо порождена другим фактором. Причинная модель этого случая — модель ложной взаимосвязи. (Пример: 79% людей, которые регулярно посещают врача, оценивают свое самочувствие как плохое. А среди тех, кто посещает врача раз в год, таких всего 15%. Вывод абсурден: чем чаще человек посещает врача, тем хуже он себя чувствует. Но есть еще гипотеза: люди с хроническими болезнями чаще обращаются к врачу и подвержены плохому самочувствию. Мы строим условные таблицы сопряженности для тех, кто здоров, и для тех, кто страдает хроническими болезнями. Мы видим, что частота посещений врача не оказывает влияние на самочувствие. Так можно понять, что метод уточнения спас нас от ложных абсурдных выводов).