
- •Лекции по математическому анализу.
- •Функции
- •Пусть и Функция удовлетворяет условию (1) и (2), т.К. Всякое вещественное есть куб некоторого вещественного числа и разные вещественные числа имеют разные кубы. Поэтому функция имеет
- •Последовательность.
- •Гиперболические функции.
- •Критерий Коши.
- •Пределы и непрерывность функции. Предел функции в точке
- •Непрерывность функции в точке.
- •Свойства функций, имеющих пределы в данной точке.
- •Свойства функций
- •Односторонние пределы и односторонняя непрерывность функции в точке.
- •Теорема 6
- •Предел функции на бесконечности.( )
- •Бмф и их свойства.
- •Свойства бмф.
- •Теорема по индукции распространяется на любое конечное число слагаемых или сомножителей.
- •Ббф. Их связь с бмф.
- •Две важные теоремы
- •Операции с непрерывными функциями.
- •Приращение аргумента и функции в точке, равносильное определение непрерывности.
- •Непрерывность элементарных функций.
- •Два замечательных предела.
- •Сравнение б.М.Ф.
- •Теоремы об эквивалентных б.М.
- •Пусть , , - б.М. При причем , - одного порядка; а тогда .
- •Если , то .
- •Свойства функций непрерывных на отрезке. Непрерывность обратной функции.
- •Теорема 4.
- •Точки разрыва функции. Их классификации.
- •Рассмотрим функцию .
- •Асимптоты графика функции.
- •Определение
- •Определение
- •Теорема
- •Непрерывность дифференцируемой функции
- •Основные правила дифференцирования
- •Дифференциальное исчисление функций одной переменной. Производная.
- •Правила дифференцирования обратной функции. Теорема
- •Производные основных элементарных функций.
- •Логарифмическое дифференцирование.
- •Дифференцирование неявной функции.
- •Другие типы неопределенностей.
- •Теорема Тейлора.
- •Разложение по формуле Маклорена некоторых элементарных функций.
- •Локальные формулы Тейлора.
- •Теоремы об возрастании и убывании дифференцируемых функций. Экстремумы.
- •Необходимое условие
- •Теорема 3
- •Если f’(X) при переходе через т. X0 сохраняет постоянный знак, то в некоторой окрестности т. X0 функция или возрастает или убывает и поэтому в т. X0
- •Понятие выпуклости графика функции на промежутке.
- •Производная и дифференциал длины дуги.
Бмф и их свойства.
Определение.
Функция
называется БМ
при
,
если
![]() ,
т.е.
,
т.е.
![]()
Пример:
![]() -
БМФ при
-
БМФ при
![]() -
БМФ при
-
БМФ при
![]() (в т. х=1).
(в т. х=1).
Из
определения предела функции при
произвольном стремлении по Коши сразу
вытекает, что функция
имеет конечный предел А
при
тогда и только тогда, когда функция (
- А)
является в этой точке БМ. Обозначая ее
через
![]() (т.е.
(т.е.
![]() приходим к следующему представлению
функции
в некоторой окрестности точки *.
приходим к следующему представлению
функции
в некоторой окрестности точки *.
![]()
![]() при
при
Свойства бмф.
I. Алгебраическая сума двух БМФ при некотором стремлении есть БМФ при том же стремлении.
П
усть
,
![]() - БМФ при
.
Это значит, что
- БМФ при
.
Это значит, что
![]()
п
оложим
![]() ,
тогда очевидно, что
,
тогда очевидно, что
![]()
![]() и следовательно
и следовательно
![]() т.е.
т.е.
![]()
Ясно, что по индукции теорема легко распространяется на любое конечное число слагаемых.
II. Произведение ограниченной функции в некоторой окрестности точки * на БМФ при есть БМФ при .
Пусть
- ограниченная функция в некоторой
окрестности
![]() ,
т.е.:
,
т.е.:
![]() Пусть далее
- БМФ при
,
т.е.
Пусть далее
- БМФ при
,
т.е.
![]()
С ледствия
ледствия
Если = С=const, то:
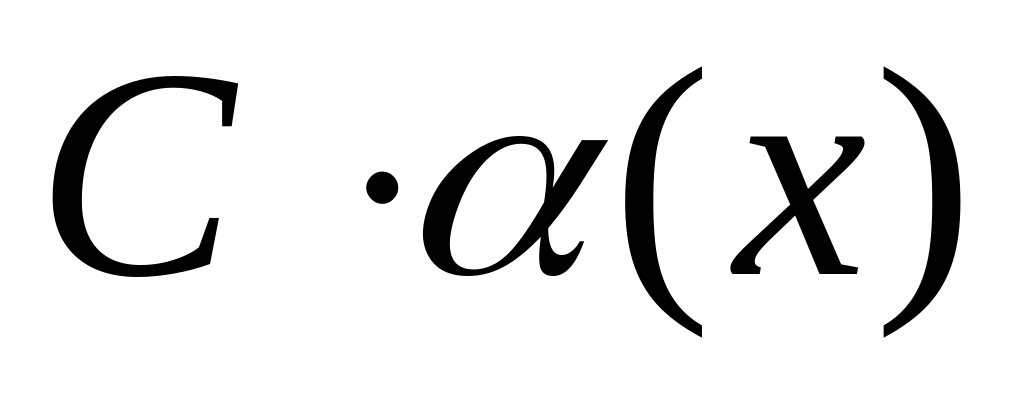 - БМФ при
где
- БМФ при
.
- БМФ при
где
- БМФ при
.Т.к. функция, имеющая конечный предел при некотором стремлении ограничена в некоторой окрестности этого стремления, то произведение такой функции на БМФ при том же стремлении есть БМФ при том же стремлении. В частности, если эта функция сама является БМ то заключаем, что произведение двух БМ есть БМ.
Этот последний результат легко обобщается по индукции на любое конечное число сомножителей.
Теорема. (об арифметических операциях с функциями, имеющие пределы).
П
усть
функции
и
![]() имеют в точке * пределы А
и В
соответственно, тогда функции
имеют в точке * пределы А
и В
соответственно, тогда функции
![]() так же имеют в т. * пределы соответственно
равные:
так же имеют в т. * пределы соответственно
равные:
![]() (в случае частного считаем, что
(в случае частного считаем, что
![]() ).
).
Пользуясь
условиями теоремы и представлением
функции, имеющей предел в точке * в виде
суммы некоторого предела и БМФ, имеем
![]() ,
где
и
- БМФ при
,
где
и
- БМФ при
![]()
![]()
![]()

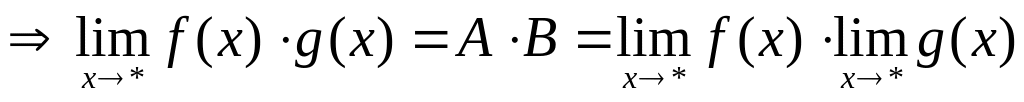
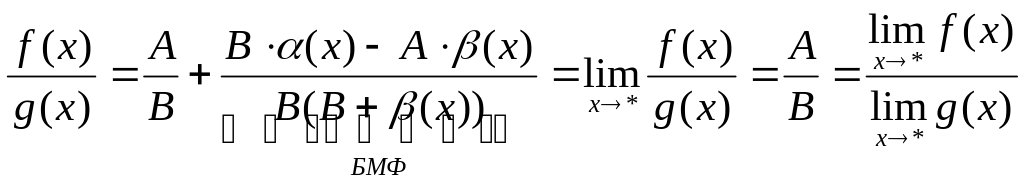 где
,
где
,
![]()
Следствия
Теорема по индукции распространяется на любое конечное число слагаемых или сомножителей.
 где
С=const
где
С=const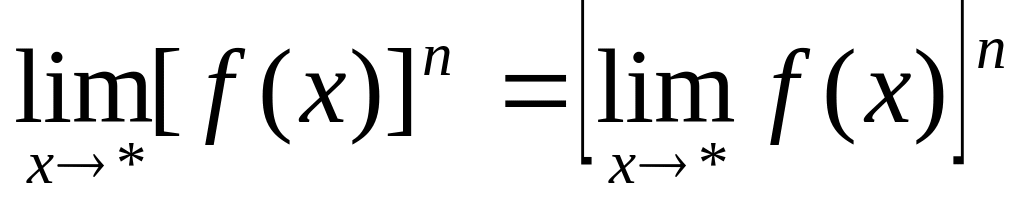
Ббф. Их связь с бмф.
Определение
Функция называется ББ при данном стремлении, если для:
![]() пишут:
пишут:
![]()
Если
![]() ,
то пишут
,
то пишут
![]() ,
если же
,
если же
![]() ,
то пишут
,
то пишут
![]() .
.
Между ББФ и БМФ в точке * имеется тесная связь, которая выражается теоремой.
Теорема:
Е
сли
функция
- БМФ в точке * и в некоторой окрестности
точки *
![]() ,
то функция
,
то функция
![]() ББФ в точке *.
ББФ в точке *.
Выберем
произвольно
,
тогда (найдется)
![]()
Аналогично доказывается, что справедлива и обратная теорема:
Теорема
Если - ББФ при , то функция - БМФ при
Две важные теоремы
Теорема 1. (о замене переменных в пределе)
Пусть:
функция переменной х преобразуется с помощью подстановки
 в функцию
в функцию
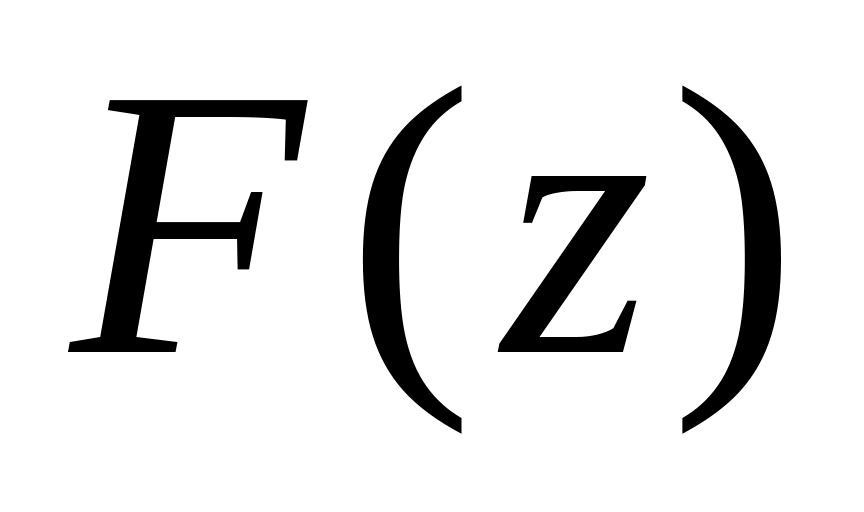 переменной z
получается
переменной z
получается
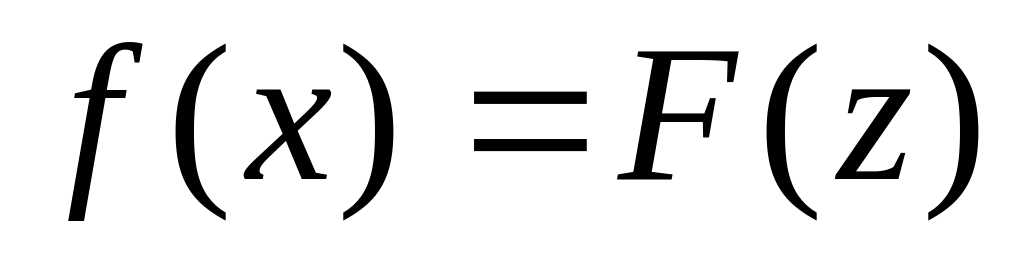
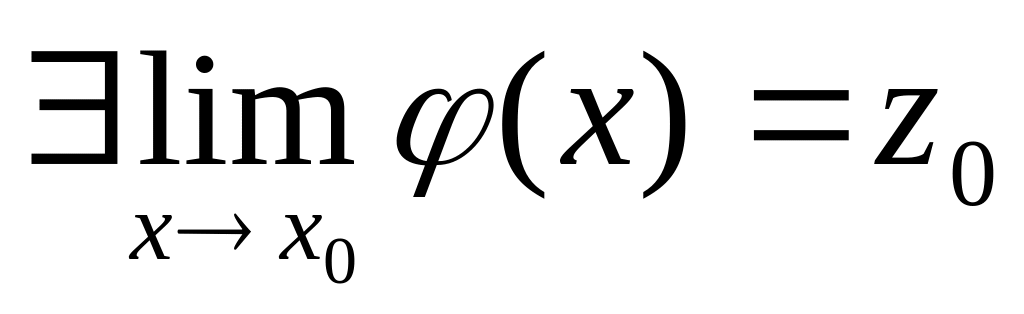 (конечный
предел) причем вблизи точки
(конечный
предел) причем вблизи точки

 тогда
тогда

Доказательство по Гейне.
Рассмотрим
произвольную последовательность
![]() .
.
П
оложим
![]() ,
тогда по Гейне последовательность
,
тогда по Гейне последовательность
![]() сходится к
сходится к
![]() ,
причем
,
причем
![]() следовательно снова по Гейне с учетом
следовательно снова по Гейне с учетом
![]() ,
имеем что последовательно
сходится к А,
т.е.
,
имеем что последовательно
сходится к А,
т.е.
Примечание
В
доказанной теореме функция
представлена как сложная функция
переменной х
посредством промежуточной переменой
![]() поэтому доказанную теорему можно
понимать как теорему о пределе сложной
функции.
поэтому доказанную теорему можно
понимать как теорему о пределе сложной
функции.
Теорема 2 (о переходе к пределу под знаком непрерывной функции)
Д обавим к условиям теоремы 1 требования непрерывности функции в точке .
Учитывая это и применяя доказательство теоремы 1 имеем:
![]()
![]()
