Логарифмическое дифференцирование.
Определение.
Логарифмической производной функции y=f(x) называется производная ее логарифма.
тогда
производная функции y=f(x)
может быть
найдена так:
.
Рассмотрим степенную функцию
Имеем
тем самым формула (7) доказана.
Применив
прием логарифмического дифференцирования,
мы можем вычислить производную
показательно-степенной функции
.
Имеем,
функции u(x)
v(x)
дифференцируемыми в т. x,
а функцию u(x)>0
в некоторой окрестности т.x:
(23).
Правило логарифмического дифференцирования рекомендуется применять на практике при дифференцировании произведения многих сомножителей.
Дифференцирование неявной функции.
Рассмотрим уравнение F(x,y)=0 относительно y.
При
некоторых условиях это уравнение
определяет единственную функцию
называемая неявной функцией, задаваемая
исходной функцией. Тогда
.
при
дифференцировании применим теорему о
производной сложной функции. В результате
получиться линейное уравнение относительно
y’
уравнение,
решая которое находим y’.
………………………………………………………………………………………………..
Примечания.
Если производные
и
удовлетворяют всем условиям доказанной
теоремы, то правило Лопиталя-Бернули
может быть повторено.Правило Лопиталя остается оправданным если
.
ЛЕКЦИЯ № |
Предел отношения функции может и без того, чтобы предел относительно их производных.
Правило Лопиталя-Бернули остается в силе, когда
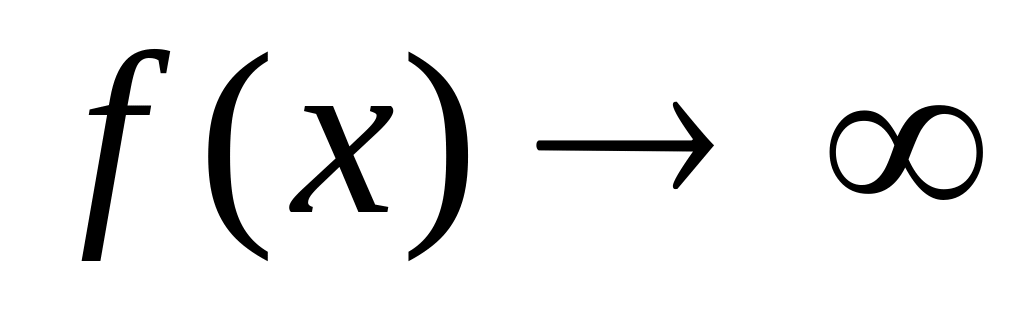и
при
.
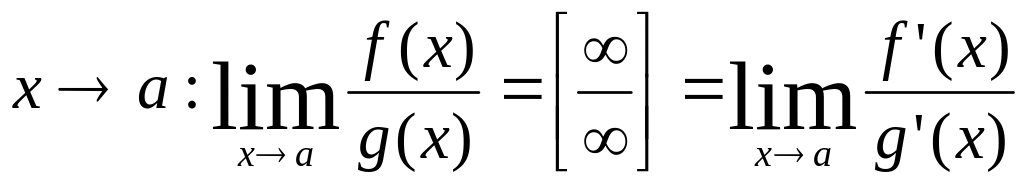Итак, правило Лопиталя-Бернули, когда
оно применимо позволяет раскрыть
неопределенности типов:
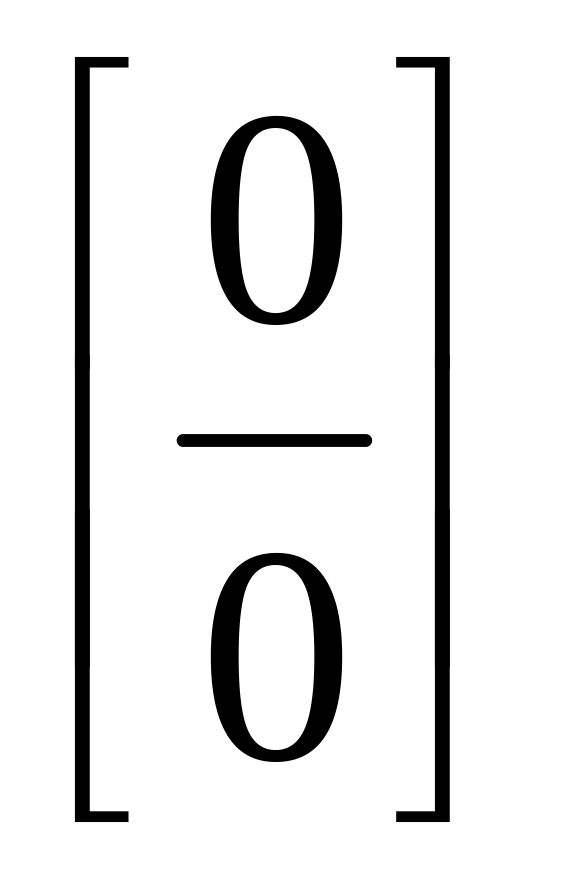и
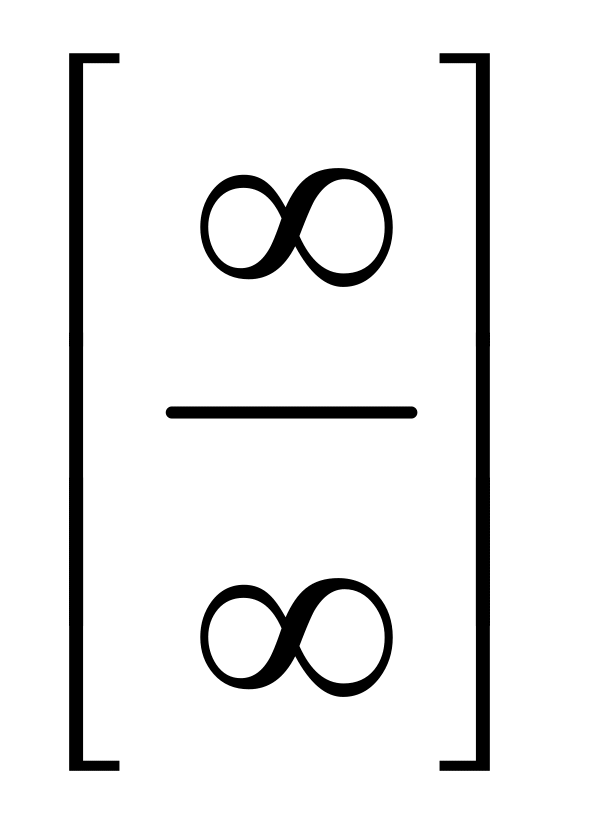.Сравнение при помощи правила Лопиталя-Бернули поведения при функции: показательно
,
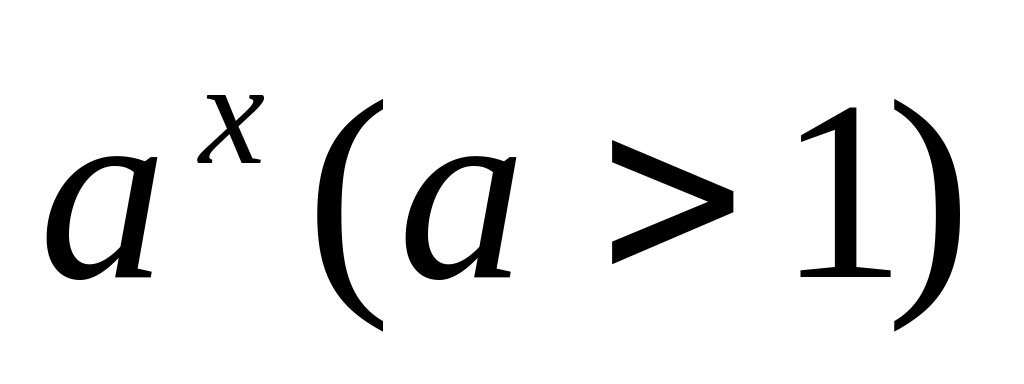степенной
и логарифмической
показывают, что показательная функция
имеет более высокий порядок роста, чем
степенная – более высокий порядок
роста чем логарифмическая.
.
Другие типы неопределенностей.
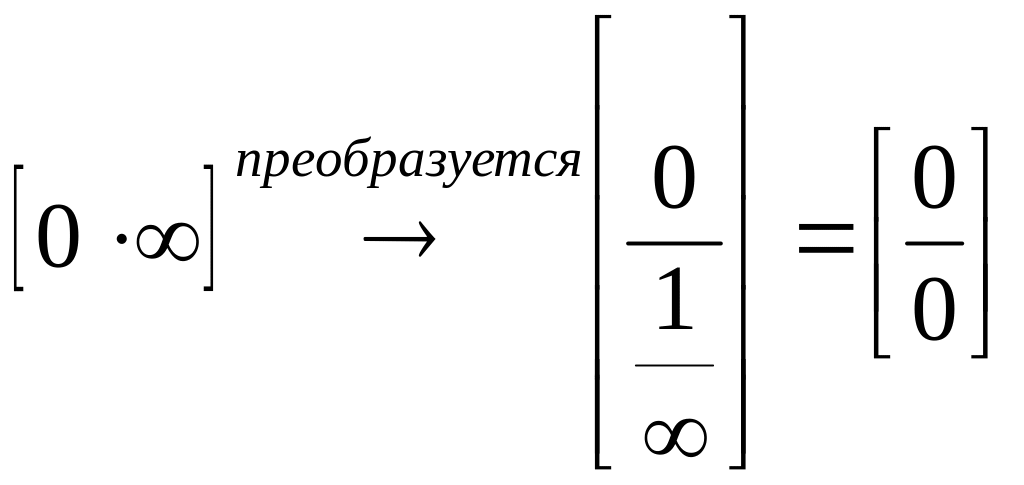или же
и применяется правило Лопеталя-Бернули.
,
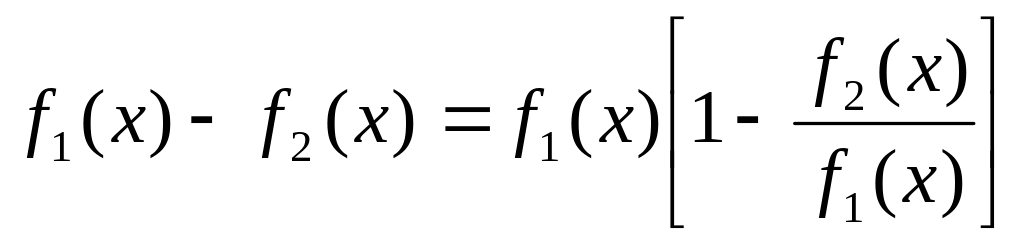если
при
,
- ББ при
,
если же
при
,
то имеем неопределенность типа
.
Неопределенности
типов
раскрываются с помощью предварительного
логарифмирования и вычисления предела
логарифма функции
что приводит к неопределенности типа
.
Примеры.
.
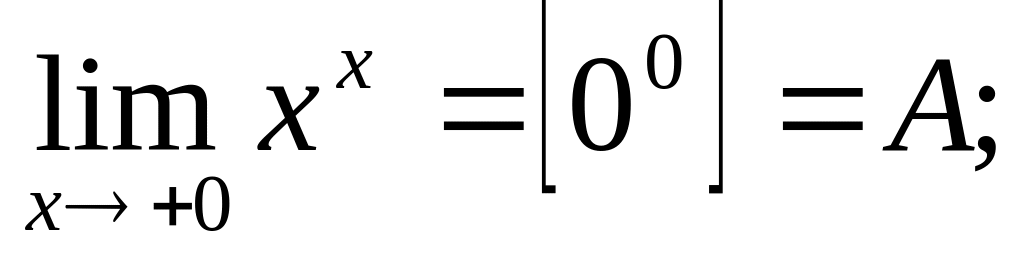
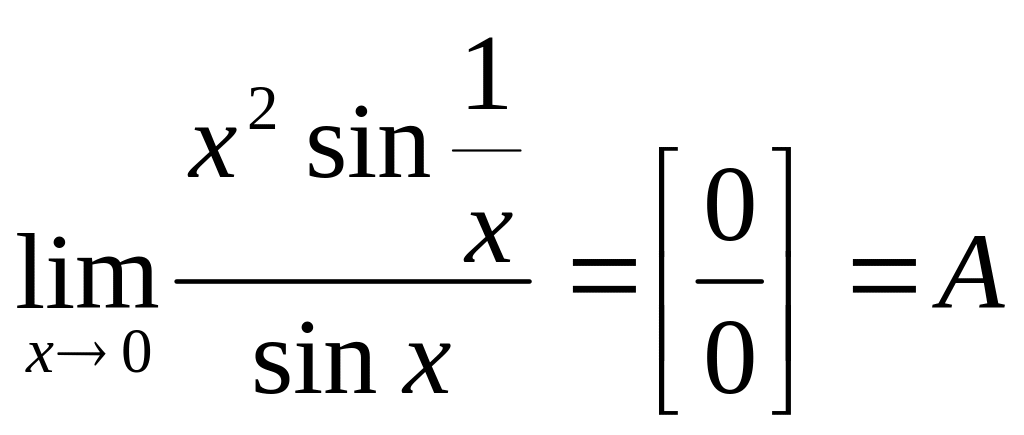Рассмотрим:
|это
отношение не имеет предела при
|
правило Лопиталя-Бернули не применимо.
Найдем предел А непосредственно.
0
Теорема Тейлора.
Пусть
функция
имеет в некоторой окрестности конечной
точки a производные
до порядка
включительно, x –
любое значение аргумента из указанной
окрестности
тогда между точками a
и x найдется точка
такая, что
(5)
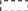многочлен
Тейлора функции
Формула (5) называется
формулой Тейлора с остаточным членом
в форме Лагранжа:
;
,
формула Тейлора с центром в точке a.
Формулу Тейлора часто записывают в
другом виде.
Положим
.
,
отсюда при n=0
получается формула Лагранжа
.
Таким образом формула
Тейлора обобщает формулу Лагранжа.
Покажем, что если функция
ограничена в окрестности точки a,
то остаточный член формулы Тейлора есть
БМ более высокого малости, чем
при
т.о.
;
(при
)
(6).
Остаточный член (6) называется остаточным членом в форме Пеано, а формула Тейлора с остаточным членом в форме Пеано называется локальной формулы Тейлора. Формула Тейлора при a=0 (с центром в 0) называется формулой Маклорена.
.
(7)
Где остаточный член
имеет: в форме Лагранжа
в форме Пеано
.