19 Вопрос Плоскость общего положения и ее проекции

Плоскость общего положения.Плоскость а, наклонная ко всем плоскостям проекций, называется плоскостью общего положения (фиг.223,а).

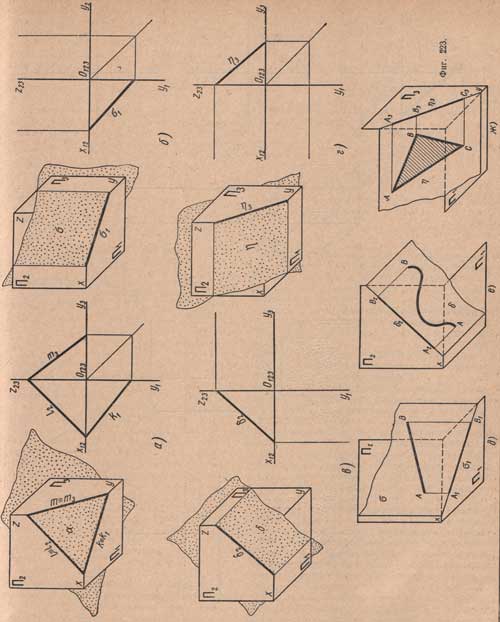
Особенностью этой плоскости является то, что всякая кривая и фигура, лежащие в этой плоскости, при проектировании не имеют ни одной проекции, равной натуральной (истинной) величине. Все ее следы k, L и m наклонены к осям х, z и у, замыкаясь, образуют фигуру треугольника, называемого треугольником следов. Такую плоскость можно изображать проекциями ее следов.

Вопрос 20:плоскоссть частного положения:

Вопрос 30.поверхности вращения.тор,точка и линия на поверхности

Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой).

Тор образуется вращением окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через её центр. Тор бывает открытый(R>r), закрытый(R=r), самопересекающийся(R<r). В сечении эллипс.

Вопрос 31. Соосными называются поверхности вращения, имеющие общую ось.

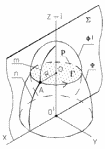
• У соосных поверхностей вращения Ф и Ф меридианы m и n , расположенные в одной осевой плоскости  ( i)пересекаются в некоторых точках, например, в точке А.

• Так как m и n вращаются вокруг оси i, то точка А описывает окружность р радиуса R = OA в плоскости Г(Г i).

• 3. Так как р Ф р Ф, то окружность р  является линией пересечения поверхностей Ф и Ф. Вывод: соосные поверхности вращения всегда пересекаются по окружности.

Вопрос 32. Метод посредника:

1. обе поверхности пересекаются третей (посредником);2. строятся линии пересечения каждой из поверхности к посреднику;3. находится точка пересечения вспомогательных линий;

В качестве посредников могут быть плоскости общего и частного положения, сферические поверхности.

Вопрос 33. Частные случаи пересечения поверхностей:

1. соосные поверхности вращения пересекаются по окружностям, лежащим в плоскости перпендикулярной их общей очи вращения;

2.одна из поверхностей (или обе) занимает проецирующее положение. Линия пересечения на соответствующей плоскости проекции будет совпадать с вырожденной поверхностью этой проекции.3. Теорема Монжа:Если 2 поверхности второго порядка описаны вокруг третьей поверхности второго порядка или вписаны в неё, то линия пересечения распадается на 2 плоские кривые второго порядка.

Вопрос 34. способ вспомогательных секущих плоскостей применяется во всех случаях, то есть каждая из пересекающихся поверхностей может быть как гранной, так и поверхностью вращения. Построение проекций линии взаимного пересечения поверхностей осуществляется в следующей последовательности:

1. Определяют на чертеже положения опорных точек кривой пересечения.

2. Определение проекций этих точек.

3. Соединение точек в плавную кривую.

Вопрос 35. Если оси поверхностей пересекаются, то вспомогательные сферы проводят из одного центра-точки пересечения осей. Линию пересечения поверхностей в этом случае строят способом вспомогательных концентрических сфер.

При построении линии пересечения поверхностей для использования способа вспомогательных концентрических сфер необходимо выполнение следующих условий

1) пересечение поверхностей вращения;

2) оси поверхностей — пересекающиеся прямые — параллельны одной из плоскостей проекций, т. е. имеется общая плоскость симметрии;

3) нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях.

Вопрос 36. Теорема Монжа:

Если 2 поверхности второго порядка описаны вокруг третьей поверхности второго порядка или вписаны в неё, то линия пересечения распадается на 2 плоские кривые второго порядка.

Вопрос37. Способ замены плоскостей проекции:

1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня.

2. Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций, расположив ее параллельно самой прямой и перпендикулярно одной из основных плоскостей проекций.

Основные задачи преобразования чертежа:

1. Прямая общего положения становится прямой уровня.

2. Прямая общего положения становится проецирующей прямой.

3. Плоскость общего положения становится проецирующей плоскостью.

4. Плоскость общего положения становится плоскостью уровня.

Для решения этих задач будем использовать метод замены плоскостей проекций, хотя каждая из них могла бы быть решена и методом вращения, и методом плоскопараллельного переноса.

вопрос38. Способ вращения вокруг проецирующей прямой более удобен при решении некоторых задач. Найдем с применением этого метода длину отрезка AB. Отрезок AB спроецируется на П2 в натуральную величину, если он будет ей параллелен. Для этого повернем его вокруг оси, проходящей через точку B до состояния параллельности П2, при этом точка A опишет дугу в горизонтальной плоскости.

Алгоритм графических построений:

Проведем ось вращения i через точку B. Ось i перпендикулярна П2;

Повернем отрезок AB до состояния параллельности оси проекций П1П2. Где A1'B1' - новая проекция AB;

Проводим вспомогательную линию на П2. Эта линия символизирует горизонтальную плоскость, в которой поворачивалась точка A;

Проводим линию связи и находим новую проекцию A2'B2' отрезка AB на П2;

A2'B2' - натуральная величина отрезка AB.