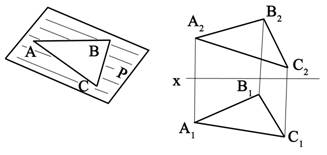
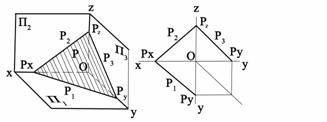
- •Вопрос1:метод проекцией. Центральное проецирование
- •Вопрос2:
- •Вопрос 3:свойство параллельного проецирования
- •Вопрос 4:оброзование комплексного чертежа точки по методу монжа
- •Вопрос 7:классификация прямых:
- •Вопрос8:следы прямой
- •Вопрос 10: прямые уровня и их проекции
- •11 Вопрос Проецирующие прямые и их проекции.
- •Вопрос 12:
- •14 Вопрос Конкурирующие точки на скрещивающихся прямых, определение относительной видимостиКонкурирующие точки.
- •Вопрос 15:
- •19 Вопрос Плоскость общего положения и ее проекции
- •Вопрос 39. Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали.
- •Вопрос 40. Развёртка - это плоскость фигуры, из которой последовательным сёртыванием или сгибанием воспроизводят заданную поверхность.
- •Вопрос 41Вид-изображ.Обращённое к наблюдателю видимой части пов-сти предмета. Допускается:невидимое части предмета штрихов.Линиями.Виды:основные,дополнительные,
- •Вопрос 42Разрезы-изобр.Предмета мысленного рассечённого одной или несколькими пл-стями.
- •Вопрос 54. Аксонометрические проекции окружностей:
- •Вопрос 55. Резьбы классифицируются по нескольким признакам:
14 Вопрос Конкурирующие точки на скрещивающихся прямых, определение относительной видимостиКонкурирующие точки.
 Как
надо рассматривать точку пересечения
одноименных проекций скрещивающихся
прямых? Она представляет собой проекции
двух точек, из которых одна принадлежит
первой, а другая – второй из этих
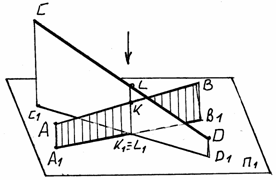
скрещивающихся прямых. Например, на рис
точка с проекциями К2 иК1 принадлежит
прямой АВ, а точка с проекциями L2 и L1
принадлежит прямой СD. Эти точки одинаково
удалены от плоскости П2, но расстояние
их от плоскости П1 различны: точка с
проекциями L2 и L1 дальше от плоскости П1
чем точка с проекциями К2 иК1 (рис 2.26.).
Как
надо рассматривать точку пересечения
одноименных проекций скрещивающихся
прямых? Она представляет собой проекции
двух точек, из которых одна принадлежит
первой, а другая – второй из этих
скрещивающихся прямых. Например, на рис
точка с проекциями К2 иК1 принадлежит
прямой АВ, а точка с проекциями L2 и L1
принадлежит прямой СD. Эти точки одинаково
удалены от плоскости П2, но расстояние
их от плоскости П1 различны: точка с
проекциями L2 и L1 дальше от плоскости П1
чем точка с проекциями К2 иК1 (рис 2.26.).
Рис. 2.26.
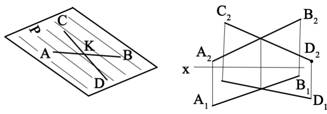
^ 2.7. Определение видимости точкиТочки с проекциями М2, М1 и N2, N1 одинаково удалены от плоскости П1, но расстояние этих точек от плоскости П2 различны. Точка с проекциями L2 и L1 принадлежащая прямой CD, закрывает собой точку с проекциями К2 иК1 прямой АВ по отношению к плоскости П2, соответствующее направление взгляда показано стрелкой у проекции L2. По отношению к плоскости П2 точка с проекцией N2, N1 прямой CD закрывает собой точку с проекциями М2, М1 прямой АВ; направление взгляда указано стрелкой внизу, у проекции N1.
Точки М2 ≡ N2,v K1 ≡ L1 – называются конкурирующими и с их помощью определяется видимость.
Вопрос 15:
.
Теорема о проецировании прямого угла.
1
Если плоскость, в которой расположен
некоторый угол, перпендикулярна к
плоскости проекций, то он проецируется
на эту плоскость проекций в виде прямой
линии.
2. Если
плоскость прямого угла не перпендикулярна
к плоскости проекций и хотя бы одна его
сторона параллельна этой Рис. 2.30.
плоскости, то прямой угол проецируется
на нее в виде прямого же угла.
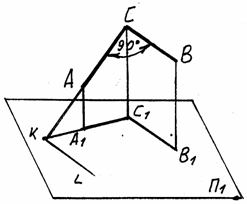 Положим,
что сторона ВС прямого угла АВС (рис.
2.30.) параллельна плоскости проекций. В
таком случае прямая СВ параллельна
С1В1.
Пусть вторая сторона (АС) прямого угла
пересекает свою проекцию А1С1 в
точке К. Проводим в плоскости проекций
через точку К прямую параллельно С1В1.
Прямая KL так же параллельна СВ, и угол
CKL получается прямым. Согласно тереме
о трех перпендикулярах угол С1KL
также прямой. Следовательно, и угол
А1С1В1прямой.
Положим,
что сторона ВС прямого угла АВС (рис.
2.30.) параллельна плоскости проекций. В
таком случае прямая СВ параллельна
С1В1.
Пусть вторая сторона (АС) прямого угла
пересекает свою проекцию А1С1 в
точке К. Проводим в плоскости проекций
через точку К прямую параллельно С1В1.
Прямая KL так же параллельна СВ, и угол
CKL получается прямым. Согласно тереме
о трех перпендикулярах угол С1KL
также прямой. Следовательно, и угол
А1С1В1прямой.
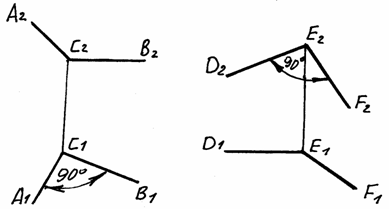 Рис.
2.31.
Этой теореме о проецировании прямого
угла соответствуют две обратных.
3.
Если проекция плоскости угла представляет
собой прямой угол, то проецируемый угол
будет прямым лишь при условии, что по
крайней мере одна из сторон этого угла
параллельна плоскости проекций. (рис.
2.31.).
4. Если
проекция некоторого угла, у которого
одна сторона параллельна плоскости
проекций, представляет собой прямой
угол, то проецируемый угол тоже
прямой.
5. Если
стороны угла одинаково наклонены к
плоскости проекций, то угол не может
равняться проектируемому углу.
Рис.
2.31.
Этой теореме о проецировании прямого
угла соответствуют две обратных.
3.
Если проекция плоскости угла представляет
собой прямой угол, то проецируемый угол
будет прямым лишь при условии, что по
крайней мере одна из сторон этого угла
параллельна плоскости проекций. (рис.
2.31.).
4. Если
проекция некоторого угла, у которого
одна сторона параллельна плоскости
проекций, представляет собой прямой
угол, то проецируемый угол тоже
прямой.
5. Если
стороны угла одинаково наклонены к
плоскости проекций, то угол не может
равняться проектируемому углу.
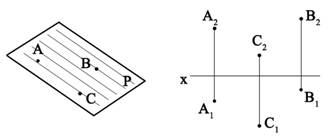
16 вопрос способы задания плоскости. Способы задания плоскости на эпюре Из курса элементарной геометрии известно, что через три точки не лежащие на одной прямой можно провести плоскость и при том только одну. Таким образом, положение плоскости в пространстве логично определить (задать) тремя точками (точки А, В, С, табл. 3.1, п1.) Кроме этого, положение плоскости в пространстве определяют: прямая АВ и точка С, не лежащая на прямой (табл. 3.1, п.2), две пересекающиеся прямые АВ и CD (табл. 3.1, п.3), две параллельные прямые АВ и CD (табл. 3.1, п.4), плоская фигура, т.е. часть плоскости, ограниченная линиями (треугольник, квадрат, круг, ромб и т.д.). На эпюре (табл. 3.1) плоскость может быть задана соответственно проекциями трех точек, не лежащих на одной прямой, прямой и точки, не лежащей на прямой, двух пересекающихся или параллельных прямых, проекцией плоской фигуры. Плоскости условимся обозначать прописными латинскими буквами, следующими за буквой P по алфавиту: R, S, T и т.д.
№ |
Задание плоскости в пространстве |
Наглядное изображение |
Эпюр |
Задание плоскости на эпюре |
1 |
Тремя точками, не лежащими на одной прямой |
|
Проекциями трех точек, не лежащих на одной прямой |
|
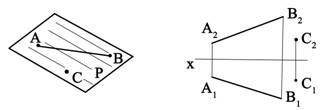
2 |
Прямой и точкой, не лежащей на прямой |
|
Проекциями прямой и точки, не лежащими на одной прямой |
|
3 |
Двумя пересекающимися прямыми |
|
Проекциями двух пересекающихся прямых |
|
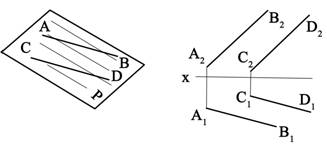
4 |
Двумя параллельными прямыми |
|
Проекциями двух параллельных прямых |
|
5 |
Плоской фигурой |
|
Проекциями плоской фигуры |
|
6 |
Следами |
|
Следами |
|
17 вопрос Характерные прямые плоскости и их проекции.
Горизонатль- это прямая линия лежащая в плоскости и паралельная горизонтальной плоскости проекции
Фронталь -это прямая линия лежащая в плоскости и паралельная фронтальной плоскости проекции
профильная-это прямая линия лежащая в плоскости и паралельная профильной плоскости проекции
18 вопрос Классификация плоскостей
1. Плоскость общего положения – непараллельна и неперпендикулярна ни одной из плоскостей проекции.
Может задаваться:
2. Плоскость уровня – плоскость параллельная какой-либо плоскости проекции;
a) горизонтальная плоскость уровня - ║П1;
Вырожденная проекция обладает собирательными свойствами.
b) фронтальная плоскость уровня - ║П2;
c) профильная плоскость уровня - ║П3.
3. Плоскости проецирующие – перпендикулярны какой-либо плоскости проекции, но непараллельны другим плоскостям проекций;
a) горизонтально-проецирующая – перпендикулярна П1, но непараллельна П2 и П3;
b) фронтально-проецирующая – перпендикулярна П2, но непараллельна П1 и П3;
c) профильно-проецирующая – перпендикулярна П3, но непараллельна П1 и П2. 18 вопрос Классификация плоскостей
1. Плоскость общего положения – непараллельна и неперпендикулярна ни одной из плоскостей проекции. Может задаваться:
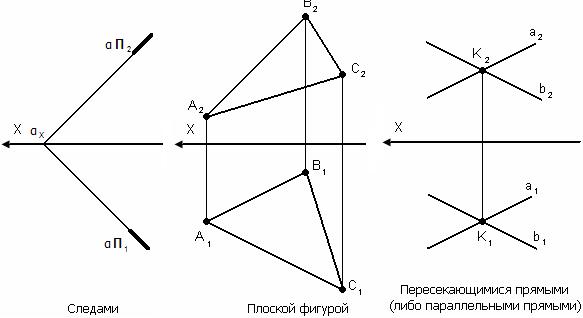
2. Плоскость уровня – плоскость параллельная какой-либо плоскости проекции; a) горизонтальная плоскость уровня - ║П1; Вырожденная проекция обладает собирательными свойствами.
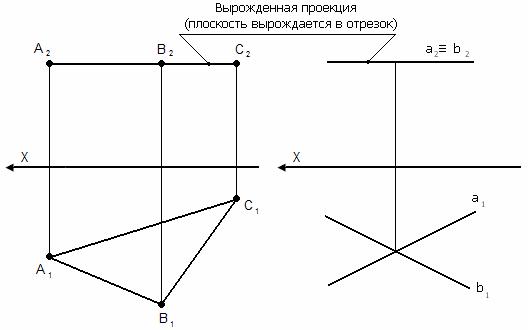
b) фронтальная плоскость уровня - ║П2;
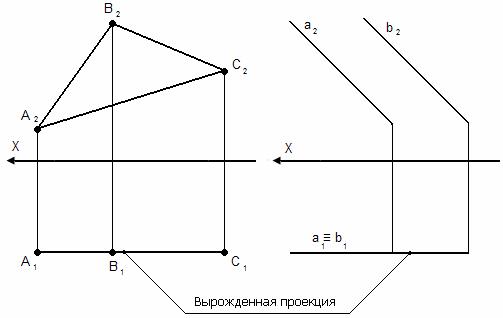
c) профильная плоскость уровня - ║П3.
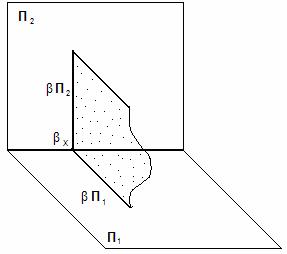
3. Плоскости проецирующие – перпендикулярны какой-либо плоскости проекции, но непараллельны другим плоскостям проекций; a) горизонтально-проецирующая – перпендикулярна П1, но непараллельна П2 и П3;
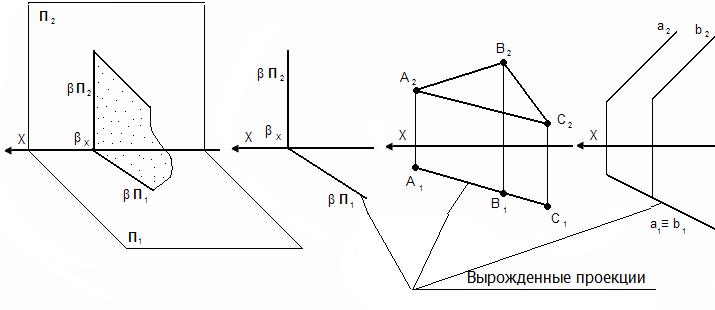
b) фронтально-проецирующая – перпендикулярна П2, но непараллельна П1 и П3;
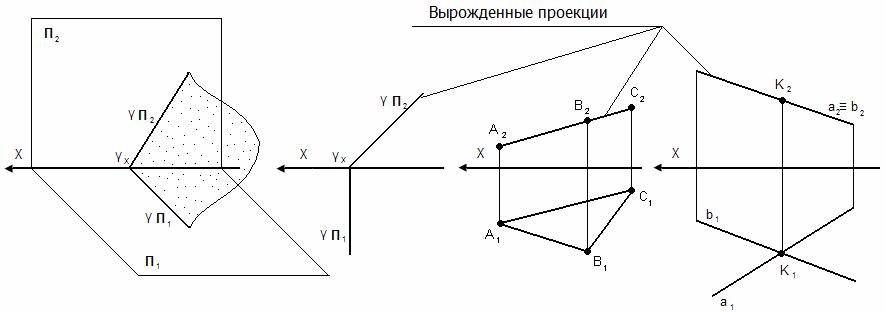
c) профильно-проецирующая – перпендикулярна П3, но непараллельна П1 и П2.