Вопрос 10: прямые уровня и их проекции

3. Прямые уровня (параллельны какой-либо плоскости проекции);

a) горизонтальная прямая уровня (параллельна П1, но неперпендикулярна П2 и П3);

h – горизонтальная прямая уровня (горизонталь)

b) фронтальная прямая уровня (параллельна П2, но неперпендикулярна П1 и П3);

f – фронтальная прямая уровня (фронталь)

c) профильная прямая уровня (параллельна П3, но неперпендикулярна П1 и П2).

р – профильная прямая уровня

11 Вопрос Проецирующие прямые и их проекции.

Проецирующей прямой называется прямая, перпендикулярная к какой–либо плоскости проекций. Прямая, перпендикулярная к горизонтальной плоскости проекций П1 называется горизонтально проецирующей. Прямая, перпендикулярная к фронтальной плоскости проекций П2 называется фронтально проецирующей. Прямая, перпендикулярная к профильной плоскости проекций П3 называется профильно проецирующей.

Вопрос 12:

Определение натуральной величины отрезка Если отрезок прямой занимает общее положение, то ни на одной основной плоскости проекций нельзя определить его истинную длину (рис. 2.15). Построить изображение отрезка в истинную величину на комплексном чертеже можно способом прямоугольного треугольника. Р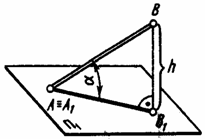 ис. 2.15Возьмем отрезок АВ (АП₁) и построим его ортогональную проекцию на горизонтальной плоскости проекции (рис. 2.16). В пространстве при этом образуется прямоугольный треугольник А₁ВВ₁, в которой гипотенузой является сам отрезок, одним катетом – разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек её отрезка не составляет труда. То можно построить на горизонтальной проекции отрезка прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отр езка АВ (рис. 2.17)

Т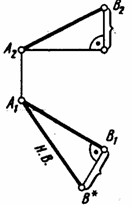 еорема: Истинная велечина отрезка прямой общего положения равна гипотенузе прям треугольника одним катетом которого является проекция отрезка на одну из плоскостей проекции,а второй катет разность расстояний концов отрезка от этой плоскости.

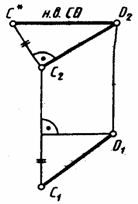
13 вопрос Взаимное положение прямых.Проекции паралельных,пересекающихся и скрещивающихся прямыхВ пространстве две прямые могут либо пересекаться, либо быть параллельными, либо быть скрещенными.Пусть нам даны пересекающиеся прямые a и b. K - точка пересечения прямых a и b. Построим чертеж в двух проекциях. Отметим точку K. Раз точка K принадлежит обеим прямым, то проводим проекции прямых а и b через одноименные проекции точки их пересечения.Свойство: если прямые пересекаются, то точки пересечения их одноимённых проекций находятся на одной линии связи.Параллельные прямые

Пусть нам даны параллельные прямые: АВ || СD. Построим первую и вторую проекции отрезков AB и CD.Свойство: параллельность отрезков прямых сохраняется в проекциях.Обратное свойство: если проекции прямых на всех плоскостях проекций параллельны, то прямые параллельны.Скрещивающиеся прямые Скрещивающиеся прямые не принадлежат одной плоскости, т.е. не пересекаются и не параллельны.Свойство: на чертеже одноименные проекции прямых, взятые отдельно, имеют признаки пересекающихся или параллельных прямых.Случай A: точки пересечения проекций прямых не лежат на одной линии связи. Хотя проекции точек A и C, B и D на одной проекции совпадают. На другой хорошо видно, что это разные точки.Случай B: прямые проецируются на одну из плоскостей в виде параллельных прямых, а на другую в виде пересекающихся прямых.