22. Индуктивность при гармоническом воздействии.

Найдем напряжение индуктивности (см. рис. 1.6, б), ток которой изменяется по гармоническому закону:

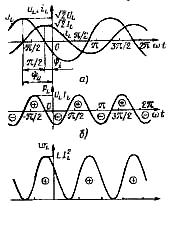. (2.73)

Связь между мгновенными значениями тока и напряжения ин­дуктивности определяется выражением (1.22). Подставляя (2.73) в (1.22), получаем:

.

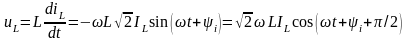причем начальная фаза напряже­ния на больше начальной фазы тока .

Действующее значение напря­жения индуктивности пропорцио­нально действующему значению тока:

.

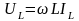Так же как и мгновенная мо­щность емкости, мгновенная мо­щность индуктивности 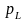при гармоническом воздействии из­меняется по гармоническому за­кону с частотой, равной

Энергия 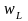, запасенная в магнитном поле индуктивности, определяется мгновенным значением тока индуктивности: .

Комплексный ток и комплексное напряжение индуктив­ности определяются выражениями:

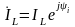; (2.76)

. (2.77)

Используя выражение (2.76), (2.77), находим комплексное сопротивление 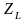и комплексную проводимость 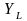индуктивности:

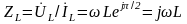; (2.78)

. (2.79)

Комплексные сопротивления и проводимости идеализированных пассивных элементов линейных цепей не зависят от амплитуды (действующего значения) и начальной фазы внешнего воздействия и определяются только параметрами соответствующих элементов и частотой внешнего воздействия.

23. Метод токов ветвей, как метод описания электрической цепи.

Метод токов ветвей (МТВ) основан на законах Кирхгофа. Число уравнений по МТВ равно количеству неизвестных токов ветвей и определяется как:

. (32)

Количество уравнений, составляемых по I закону Кирхгофа равно:

. (33)

Количество уравнений, составляемых по II закону Кирхгофа равно:

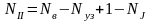. (34)

При составлении уравнений по II закону Кирхгофа следует выбирать независимые контуры, не содержащие источников тока.

Метод контурных токов (МКТ) позволяет уменьшить количество уравнений до числа:

. (35)

Ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви.

Выбирают и обозначают известные и неизвестные контурные токи.

Известные контурные токи – эти токи можно считать совпадающими с соответствующими токами источников тока и они являются заданными по условию задачи.

Неизвестные контурные токи – определяются по II закону Кирхгофа и для них составляется система уравнений в виде:

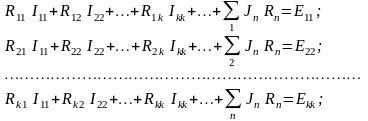(36)

где R_kk – собственное сопротивление контура k; R_km – общее сопротивление контуров k и m, причем, если направление контурных токов в общей ветви для контуров k и m совпадают, то R_km >0, в противном случае R_km<0; E_kk – алгебраическая сумма ЭДС, включенных в ветви, образующие контур k; R_n – общее сопротивление ветви контура n с контуром, содержащим источник тока.

I₁₁, I₂₂ – неизвестные контурные токи;

J₁₁ = J – известный контурный ток;

I₁, I₃, I₄ – неизвестные токи в ветвях, которые

определяются через контурные токи в виде:

I₁ = – I₁₁, I₃ = J₁₁ – I₂₂, I₄ = I₂₂.

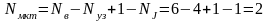
Система уравнений для контурных токов:

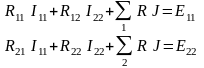, где

R₁₁ = R₁, R₁₂ = R₂₁ = 0, R₂₂ = R₃ + R₄, , , 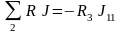E₁₁ = E₁ + E₂, E₂₂ = –E₁ – E₂.

Перепишем уравнения в компактном виде:

.

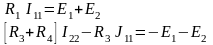Окончательно получаем:

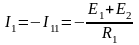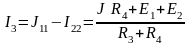(А), (А), (А).

Другой вариант

20. Сопротивление при гармоническом воздействии.

Электрической цепью называют совокупность устройств, предназначенных для прохождения тока и описываемых с помощью понятий электрического тока и электрического напряжения. Электрическая цепь содержит в себе как источники, так и приемники. Источниками электрической цепи являются устройства, которые создают (генерируют) токи и напряжения. Приёмниками электрической цепи называют устройства, потребляющие или преобразующие электрическую энергию в другие виды энергии.

В основе анализа электрических цепей лежит принцип моделирования: при анализе электрической цепи создаётся физическая модель, содержащая некоторую основную информацию об этой цепи. Далее формируется математическая модель – система уравнений, с помощью которых описывается физическая модель.

К пассивным элементам относятся: резистивное сопротивление, индуктивность и емкость.

Р езистивным сопротивлением называют идеализированный элемент, обладающий свойством необратимого рассеивания энергии.

Условное обозначение:

Математическая модель определяется законом Ома:

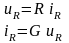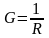, где (5)

где R – сопротивление [Ом], G – проводимость [См].

Уравнение (5) определяет вольт-амперную характеристику (ВАХ) резистивного элемента.

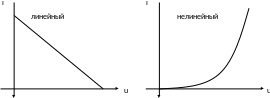
Мощность в резистивном сопротивлении определяется соотношением вида:

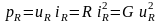. (6)