18. Комплексные сопротивление и проводимость участка цепи.

В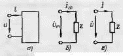 ы­делим участок этой цепи, имеющий два внешних зажима и не содержащий источников энер­гии (рис. 2.7, а). Ток i и напря­жение и на зажимах этого участка являются гармони­ческими функциями времени:

По определению, комплексным входным сопротивле­нием (комплексным сопротивлением) Z пассивного участка цепи называется отношение комплексной амплитуды напряжения на за­жимах участка цепи к комплексной амплитуде тока: 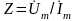. Выражая комплексные амплитуды напряжения и тока через со­ответствующие комплексные действующие значения 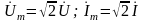, устанавливаем, что комплексное сопротивление пассив­ного участка цепи может быть также найдено как отношение комп­лексных действующих значений напряжения и тока:

Комплексное входнoe сопротивление пассивного участка цепи представляет собой в общем случае комплексное число; поэтому оно может быть представлено в показательной или алгебраической

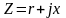
Величины 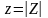и 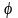называются соответственно модулем и аргументом комплексного сопротивления, величины r и x — его вещественной (резистивной) и мнимой (реактивной) составляющими (модуль комплексного входного сопротивления цепи z называется также полным входным сопротивлением). Представляя комплексные амплитуды и комплексные действующие значения напряжений и то­ков в показательной форме, из (2.42) и (2.43) находим: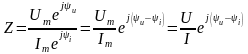 . Величина, обратная комплексному входному сопротивлению, называется комплексной входной проводимостью участка цепи:

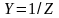
полной входной проводимостью цепи, является вели­чиной, обратной модулю комп­лексного входного сопротивления: ,

19. Комплексная схема замещения цепи. Законы Ома и Кирхгофа в комплексной форме.

Зная комплексное сопротивление (комплексную проводимость) участка цепи и одну из приложенных к данному участку цепи величин — ток 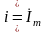, или напряжение , можно, используя (2.42), (2.50), найти неизвестное напряжение или неизвестный ток исследуемого участка

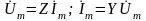. (2.56)

Аналогично определяют комплексные действующие значения напряжения и тока на зажимах участка цепи: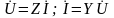 . (2.57)

Выражения (2.56), (2.57) по структуре напоминают соотношения между мгновенными значениями напряжения и тока на зажимах линейного сопротивления (1.9), (1.10) и являются математической записью закона Ома в комплексной форме. В отличие от выражений уравнения (2.56), (2.57) являются алгебра­ическими.

Используя закон Ома в комплексной форме, каждому участку линейной электрической цепи, составленному из идеализированных пассивных элементов и имеющему два внешних вывода, в том числе любому идеализированному пассивному двухполюсному элементу можно поставить в соответствие комплекс­ную схему замещения, на которой рассматриваемый участок цепи представлен комплексным сопротивлением или проводимостью, а токи и напряжения на его зажимах — комплексными ампли­тудами

или комплексными действующими зна­чениями.

Первый закон Кирхгофа в комплексной форме устанавливает связь между комплексными изображениями токов в каждом из узлов моделирующей цепи: сумма комплексных амплитуд (комп­лексных действующих значений) токов всех ветвей, подключенных к каждому из узлов электрической цепи, равна нулю: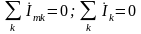 , (2.58)

где k — номер ветви, подключенной к рассматриваемому узлу.

Второй закон Кирхгофа в комплексной форме определяет связь между комплексными изображениями напряжений ветвей, входя­щих в произвольный контур электрической цепи: сумма комплекс­ных амплитуд (комплексных действующих значений) напряжений всех ветвей, входящих в любой контур моделирующей цепи, равна нулю:

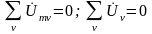, (2.59)

где — номер ветви, входящей в рассматриваемый контур.

В ряде случаев удобно использовать другую формулировку вто­рого закона Кирхгофа в комплексной форме: сумма комплексных изображений напряжений на всех элементах любого контура моде­лирующей цепи, кроме источников напряжении, равна сумме комплексных изображений ЭДС всех входящих в контур источников напряжения:

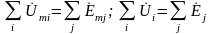. (2.60)

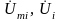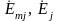где — комплексные изображения напряжений всех элементов контура, за исключением источников напряжения; — комплексные изображения ЭДС источников напряжения, действующих в рассматриваемом контуре.

В связи с тем что выражения (2.58) — (2.60) непосредственно вытекают из соотношений (1.39) — (1.41), при суммировании комп­лексных изображений токов и напряжений ветвей электрической цепи в выражениях (2.58) — (2.60) сохраняются те же правила зна­ков, что и при суммирование мгновенных значений токов и напря­жений.

Законы Кирхгофа были сформулированы только для мгновенных значений, комплексных амплитуд и комплексных действующих значений токов и напряжений. Они не выполняются для амплитуд и действующих значений соответствующих величин.