Вопрос 18: Случайная величина, равномерно распределенная на отрезке.

Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке  , где  , если её плотность   имеет вид:

Пишут:  . Иногда значения плотности в граничных точках   и   меняют на другие, например  или  . Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей

Функция распределения

Интегрируя определённую выше плотность, получаем:

Так как плотность равномерного распределения разрывна в граничных точках отрезка  , то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:

.

Производящая функция моментов

Простым интегрированием получаем производящую функцию моментов:

,

откуда находим все интересующие моменты непрерывного равномерного распределения:

,

,

.

Вообще,

.

Стандартное равномерное распределение

Если   и  , то есть  , то такое непрерывное равномерное распределение называют стандартным.

Имеет место элементарное утверждение:

Если случайная величина   и  , то  .

Таким образом, имея генератор случайной выборки из стандартного непрерывного равномерного распределения, легко построить генератор выборки любого непрерывного равномерного распределения.

Более того, имея такой генератор и зная функцию обратную к функции распределения случайной величины, можно построить генератор выборки любого непрерывного распределения (не обязательно равномерного) с помощью метода обратного преобразования. Поэтому стандартно равномерно распределённые случайные величины иногда называют базовыми случайными величинами.

Вопрос 19: Случайный вектор и основные его характеристики. Независимые случайные величины.

Случайный вектор в теории вероятностей — вектор  , компонентами которого служат случайные величины  , совместное распределение которых задается вероятностями

где   — борелевское подмножество, которые однозначно определяются n-мерной функцией распределения

Абсолютно непрерывное распределение случайного вектора   определяется плотностью  :

Дискретное распределение случайного вектора   определяется не более, чем счётным числом вероятностей   так, что

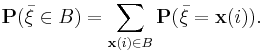
Вопрос 20: Неравенство Чебышева. Теорема Чебышева.

При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющей конечную дисперсию, сходится по вероятности к ее математическому ожиданию.

Теорема Чебышёва в теории вероятностей — теоретическая основа закона больших чисел; широкое обобщение теоремы Бернулли.

Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное число e, вероятность неравенства

будет сколь угодно близка к единице, если число случайных величин достаточно велико.

Теорема (Теорема Чебышёва). Для независимых случайных величин   соотношение

(при любом   и  ) верно при весьма общих предположениях:

Лемма Чебышева:

пусть кси > или =0 - неотрицательная случайная величина, имеющая мат. ожидание.

P(кси>или=t)<или=Mкси/t, t>0

кси - дискретная случайная величина, х1,....,хn - возможные значения случайной величины.

Mкси(мат.ожидание)=сумма(xi*pi) - вероятность, с которой принимают соответствующие значения.

 Пусть Х – случайная величина. Для любого положительного числа а справедливо неравенство

Неравенство Чебышева:

Чем меньше дисперсия, тем меньше вероятность больших отклонений.