Вопрос 12: Локальная функция и теорема Лапласа.

Для любого числа испытан вероятностей связанных со схемой Бернулли, вычисляется Локальная/Интегральная теорема Лапласа. Их применяют для точности, если каждое из чисел np и n(1-p)достигло нескольких десятков. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0<р<1), событие наступит ровно m-раз, приближенно равна P(_n =m)=

где Z=m-np/npq, (t)=(1/2П)*e^-t2/2

график функции: непрерывен, неотрицателен, всюду определена, четная, и при наибольшем значении принимает наименьшее (т.е. при t=0 наим. знач.)

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

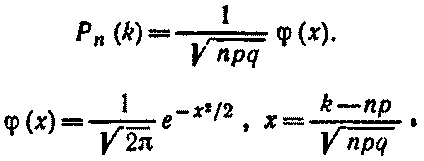
Свойства функции ϕ(x):

1. ϕ( x )> 0

2. ϕ( − x) = ϕ( ) x

3. lim ϕ( x )=0

Вопрос 13: Интегральная функция и теорема Лапласа.

Пусть производится n независимых опытов, в каждом из которых вероятность наступления события А одна и та же и равна  . Пусть m - число появления события A в n опытах. Тогда для достаточно больших n случайная величина m имеет распределение, близкое к нормальному с параметрами a=M(m)=np,  .

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P(k₁;k₂)=Φ(x'') - Φ(x')

Здесь

-функция Лапласа

Вопрос 14: Распределение Пуассона.

Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Выберем фиксированное число   и определим дискретное распределение, задаваемое следующей функцией вероятности:

,

где

 обозначает факториал числа  ,

 — основание натурального логарифма.

Тот факт, что случайная величина   имеет распределение Пуассона с параметром  , записывается:  .

Распределение Пуассона используется при анализе результатов выборочных маркетинговых обследований потребителей, расчете оперативных характеристик планов статистического приемочного контроля в случае малых значений приемочного уровня дефектности, для описания числа разладок статистически управляемого технологического процесса в единицу времени, числа «требований на обслуживание», поступающих в единицу времени в систему массового обслуживания, статистических закономерностей несчастных случаев и редких заболеваний, и т.д.

Случайная величина распределяется по закону Пуассона - это дискретная случайная величина множество значений которой целые неотрицательные числа, а вероятности, с которыми они принимаются:pi=(ⁱ/i!)e^-, 0. случайная величина имеет распределение П(),если Р(=i)=(ⁱ/i!)e^-.

Найдем Мат.Ожидание. М=_i=0^(xipi)=i*(ⁱ/i!)e^-=e^-i(ⁱ/i!)= e^-*(^i-1/(i-1)!)= e^-_k=0(^k/k!)= e^- e^= .

Вывод: если случайная величина  распределяется по закону Пауссона, то М=; D=, то параметр -среднее число заявок.

Пример случайной величины, распределяется по закону Пуассона – число заявок, поступивших на станцию обслуживания за время т.