- •9.1.4. Оптическая передаточная функция (опф)
- •График функции передачи модуляции
- •Введение
- •Метод дифференцирования закона функционирования
- •Метод разложения закона функционирования в степенной ряд
- •X / r . Разлагая arctg в степенной ряд, ограниченный первыми двумя его
- •Векторно-матричный метод
- •Геометрический метод
- •Метод преобразования исходной схемы
- •Метод плана малых перемещений
- •Заключение
- •Функция передачи модуляции
Оптическая передаточная функция. Определение оптической передаточной функции (тест-объект, его пространственная частота, модуляция). Коэффициент передачи модуляции. Функция передачи модуляции.
9.1. Основные характеристики структуры изображения (ФРТ, ОПФ)
9.1.1. Основные понятия
Передача структуры предмета или изображения – это отображение оптической системой мелких деталей объекта. Математически можно описать зависимость распределения интенсивности от пространственных координат на предмете и изображении в виде функций и .
Свойство линейности
![]()
Изображение суммы объектов равно сумме изображений каждого объекта:
Изображающие оптические системы полностью линейны.
Свойство инвариантности к сдвигу (условие изопланатизма)
При смещении точки ее изображение только смещается на пропорциональную величину:
![]()
где ![]() – увеличение.
– увеличение.
Изопланатическая зона – это зона, в пределах которой соблюдается условие изопланатизма. Мы будем рассматривать структуру изображения в пределах одной изопланатической зоны.
9.1.2. Функция рассеяния точки
Функция рассеяния точки (ФРТ, point spread function, PSF) – это функция, описывающая зависимость распределения освещенности от координат в плоскости изображения, если предмет – это светящаяся точка в центре изопланатической зоны.
Изображение
всего предмета будет представлять собой
сумму изображений ![]() каждой
его точки:
каждой
его точки:
Функция изображения есть свертка функции предмета с функцией рассеяния точки:
|
или |
|
9.1.3. Гармонический периодический объект
Предмет кроме разложения на отдельные точки можно разложить на другие элементарные части – периодические решетки.
Периодическая решетка – это структура с белыми и черными полосами.
Гармоническая периодическая решетка – это структура, интенсивность которой описывается гармонической функцией:
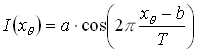
где ![]() –
вещественная амплитуда,
–
вещественная амплитуда, ![]() –
сдвиг,
–
сдвиг, ![]() –
период,
–
период, ![]() –
угол ориентации.
–
угол ориентации.
Интенсивность гармонической
решетки в комплексной форме:
![]()
где ![]() – пространственная
частота,
– пространственная
частота, ![]() –
комплексная амплитуда.
–
комплексная амплитуда.
или
![]() где
где ![]() –
частота в направлении
–
частота в направлении ![]() ,
, ![]() –
частота в направлении
–
частота в направлении ![]() .
.
Если разложить предмет на элементарные гармонические объекты, то изображение – это совокупность изображений элементарных объектов.
Изображение гармонического объекта:
|
где ![]() ,
, ![]() –
некоторая функция, зависящая от
пространственных частот.
–
некоторая функция, зависящая от
пространственных частот.
9.1.4. Оптическая передаточная функция (опф)
Оптическая
передаточная функция (optical
transfer function, OTF) ![]() характеризует
передачу структуры предмета оптической
системой как функция пространственных
частот:
характеризует
передачу структуры предмета оптической
системой как функция пространственных
частот:
|
ОПФ связана с ФРТ интегральным преобразованием – преобразованием Фурье:
![]() или
или ![]() где
где ![]() –
обозначение Фурье преобразования:
–
обозначение Фурье преобразования:

ФРТ показывает, как оптическая система изображает точку, а ОПФ показывает, как оптическая система изображает гармоническую решетку, то есть как меняется комплексная амплитуда решетки в зависимости от частоты.
Оптическая передаточная функция – это комплексная функция:
|
Модуль
ОПФ ![]() называется модуляционной
передаточной функцией (МПФ)
или частотно-контрастной
характеристикой(ЧКХ).
называется модуляционной
передаточной функцией (МПФ)
или частотно-контрастной
характеристикой(ЧКХ).
Аргумент
(фаза) ОПФ ![]() называется фазовой
передаточной функцией (ФПФ)
или частотно-фазовой
характеристикой(ЧФК).
называется фазовой
передаточной функцией (ФПФ)
или частотно-фазовой
характеристикой(ЧФК).
Частотно-контрастная
характеристика показывает передачу
вещественной амплитуды гармонического
объекта:
![]() где
–
амплитуда на предмете,
где
–
амплитуда на предмете, ![]() –
амплитуда на изображении.
–
амплитуда на изображении.
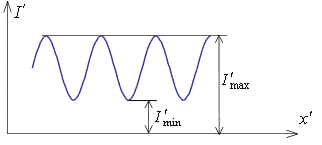
Контраст гармонического объекта:
|
|
Если ![]() ,
то
,
то ![]() – абсолютный
контраст.
Если
– абсолютный
контраст.
Если ![]() ,
то
,
то ![]() –
изображение практически отсутствует.
–
изображение практически отсутствует.
Изображение
нельзя зарегистрировать или увидеть в
случае, если ![]() где
где ![]() –
порог контраста, зависящий от приемника
изображения (например, для глаза
–
порог контраста, зависящий от приемника
изображения (например, для глаза ![]() ).
).
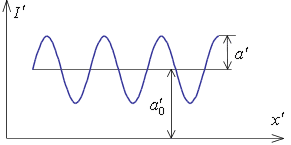
Контраст
для изображения гармонического объекта
может быть выражен через постоянную Если
где |
|
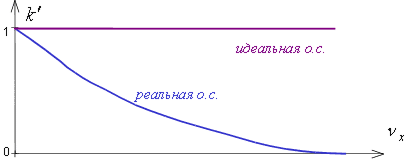
Частотно-контрастная характеристика показывает зависимость контраста изображения гармонической решетки от частоты решетки, если считать, что на предмете контраст единичный. Для идеальной оптической системы ЧКХ – прямая, параллельная оси. Для ближнего
типа предмета
или изображения пространственная
частота |
|
График функции передачи модуляции
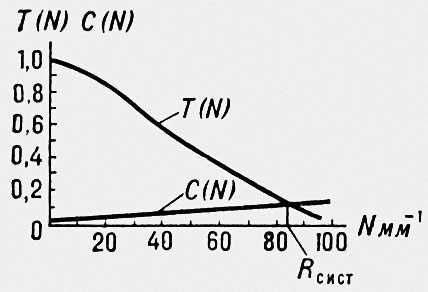 График
функции передачи модуляции, на котором
коэффициент передачи модуляции T(N)
представлен как функция пространственной
частоты решётки N (величины,
обратной её периоду). Кривая C(N)
контрастной чувствительности глаза
характеризует остроту зрения. Точка
пересечения этих двух кривых даёт
величину разрешающей способности
фотографирующей системы Rсист.
График
функции передачи модуляции, на котором
коэффициент передачи модуляции T(N)
представлен как функция пространственной
частоты решётки N (величины,
обратной её периоду). Кривая C(N)
контрастной чувствительности глаза
характеризует остроту зрения. Точка
пересечения этих двух кривых даёт
величину разрешающей способности
фотографирующей системы Rсист.
ЛЕКЦИЯ №7
ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ПЕРВИЧНЫХ
ПОГРЕШНОСТЕЙ ОПТИЧЕСКИХ ПРИБОРОВ
Введение
На предыдущей лекции была приведена классификация погрешностей,
согласно которой существуют первичные погрешности приборов, которые
представляют собой отклонения от номинальных значений конструктивных
параметров и характеристик деталей, изменения влияющих параметров
(например, температуры), отклонения от расчетного значения функции
преобразования сигнала, методические ошибки входного сигнала и т.д.
Каждая первичная погрешность влияет на точность прибора, и это влияние
называют частичной погрешностью.
Частичная погрешность y равна произведению первичной погрешности
x на некоторую функцию А: y Ax . Эта функция называется
передаточной функцией первичной погрешности. Суммарная погрешность
выходного сигнала прибора (точность результата функционирования) равна
алгебраической сумме частичных погрешностей. Поэтому важно уметь
находить передаточные функции, которые позволяют не только определить
численные значения погрешностей, но и исследовать качественные и
количественные зависимости ошибок от конструктивных параметров,
диапазона и условий функционирования устройства.
Для получения передаточных функций обычно используют
аналитические и графо-аналитические методы. К первому типу относят
метод дифференцирования функции преобразования сигнала, метод
разложения функции преобразования в ряд, векторно-матричный метод. Ко
второму типу – геометрический метод, метод преобразования исходной
схемы и метод плана малых перемещений.

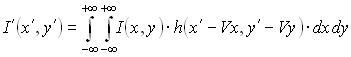
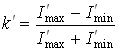
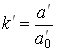
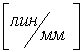 .
Для дальнего
типа пространственная
частота измеряется в
.
Для дальнего
типа пространственная
частота измеряется в