12. Колебания-процессы, повторяющиеся с течением времени.

Формула     гармонического    колебания у = A sin (ωt + φ)  определяет у как функцию  времени  t.  Максимальное    значение этой функции равно, очевидно, А, а минимальное (— А). Следовательно,  все   значения   этой   функции   заключены  между —А и A. Поэтому А  называется амплитудой колебания.

Переменный угол ωt + φ называется фазой колебания. Начальная фаза колебанияφ всегда положительна и меньше 2π.

Время Т, Период-время одного полного колебания.

Посмотрим, как выражается период гармонического колебания Т через амплитуду А, угловую скорость ω и начальную фазу φ.

За время Т точка М пройдет путь ωТ радианов. Но этот путь вместе с тем равен длине окружности, то есть 2π радианам. Поэтому ωТ = 2π, откуда

Т = ^2π/_ω.              (2)

Таким образом, период гармонического колебания обратно пропорционален угловой скорости. Он не зависит ни от амплитуды, ни от начальной фазы колебаний.

Величину, обратную периоду колебания, принято называть частотой колебания и обозначать буквой ν . (греческая буква, читается : ню ).Частота гармонического колебания (1) равна

ν = ¹/_T =^ω/_2π.                        (3)

Эта величина показывает, сколько колебаний совершает точка в течение одной секунды.

        дважды продифференцируем его по времени:

        

        

        Видно, что выполняется следующее соотношение:

               ⁽²⁾

которое и называется уравнением свободных гармонических колебаний (в дифференциальной форме). Уравнение (1) является решением дифференциального уравнения (2). Поскольку уравнение (2) - дифференциальное уравнение второго порядка, необходимы два начальных условия для получения полного решения (то есть определения входящих в уравнение (1) констант A и _); например, положение и скорость колебательной системы при t = 0.

13. Если на колебательную систему не действуют внешние силы, то такие колебания называются свободными.

Гармоническое колебание описывается формулой, выражающей  зависимость смещения x от времени t: x=A sin(wt+f).  Скорость - производная от смещения: v=x'=Aw cos(wt+f).  Ускорение - производная от скорости: a=v'=-Aw^2 sin(wt+f).

Скорость и ускорение точки, совершающей гармонические колебания

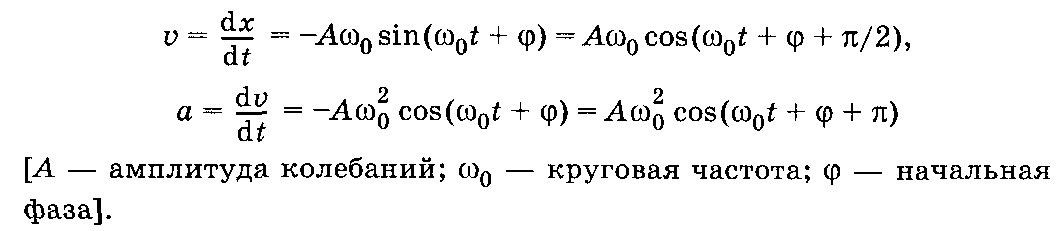
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.

Кинетическая энергия обозначается буквой E_k.

                                                         (2)

Тогда равенство (1) можно записать в таком виде:

A = E_k2 – E_k1.                                                            (3)

Теорема о кинетической энергии:

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой т равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:

                                   (4)

Физический смысл кинетической энергии:

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующаяна покоящееся тело, чтобы сообщить ему эту скорость.

Потенциальная энергия   — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.

Потенциальная энергия   в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где   — масса тела,   — ускорение свободного падения,   — высота положения центра масс тела над произвольно выбранным нулевым уровнем.

14. Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида   в природе невозможен.

Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

Общая формула для добротности любой колебательной системы:

,

15. Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения^[1]. 

Период колебаний физического маятника:

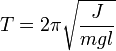
где   — момент инерции маятника относительно оси вращения,   — масса маятника,   — расстояние от оси вращения до центра масс.

Период колебаний математического маятника:

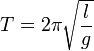
где   — длина подвеса (к примеру нити),   — ускорение свободного падения.

Приведённая длина — это условная характеристика физического маятника. Она численно равна длине математического маятника, период которого равен периоду данного физического маятника.

Приведённая длина вычисляется следующим образом: где I — момент инерции относительно точки подвеса, m — масса, a — расстояние от точки подвеса до центра масс.

16. Идеальный газ-газ, который удовлетворяет следующим требованиям: 1. Обьемом молекул можно пренебречь,2. Молекулы не взаимодействуют друг с другом. 3. Столкновение друг с другом и о стенки сосуда являются абсолютно упругими.

pV=НюRT

P= 2mv*1/6N=1/3mvnV=1/3mv2*nSt=1/3mnv2=1/3mnv2

17. Внутренняя энергия идеального газа складывается только из кинетической энергии его молекул.

Способы изменения внутренней энергии: сообщить теплоту, совершить над системой работу.

Первое начало термодинамики Q=дельтаU + A

18. Теплоемкость газа-количество теплоты, которое необходимо сообщить этому телу, чтобы увеличить его температуру на 1 градус.

Молярная теплоемкость-величина, равная количеству теплоты, которое необходимо для нагревания 1 моля вещества на 1 градус. Дж\моль к

Удельная теплоемкость- величина, равная количеству теплоты, которое необходимо для нагревания 1 кг вещества на 1 градус. Дж/кг к

Cp=i+2/2 R Cv=i/2 R

Cp=Cv+R –уравнение Майера

19. Изотермический процесс. T-const

Pv=p1v1

2. Изобарный. P=const

V/T=V2/T2

3. Изохорный процесс. V=const

P/T=P2/T2

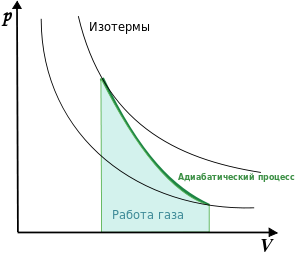
20. Адиабатный процесс- процесс, при котором система не получает теплоту.

дельтаU=-A

V^f-1 *T=const

Pv^f=const уравнение Пуассона.

Показатель адиабаты (иногда называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении ( ) к теплоёмкости при постоянном объёме ( ).

21. Процесс называется обратимым, если при совершении его сначала в прямом, а затем в обратном направлении не останется никаких изменений.

 Отношение количества переданной теплоты к температуре теплоотдатчика или теплоприемника называется приведенной теплотой.

Энтропия-мера беспорядка.

Постулат Клаузиуса-Невозможен процесс, единственным результатом которого была бы передача тепла от более холодного тела более нагретому.

Второй закон термодинамики: энтропия замкнутой системы не убывает.

Теорема Больцмана-на каждую степень свободы приходится одинаковая энергия

22. Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.

1)КПД обратимого цикла Карно, осуществляемого между двумя источниками теплоты, не зависит от свойств рабочего вещества, с помощью которого этот цикл осуществляется.

2) КПД необратимого цикла Карно всегда меньше обратимого цикла Карно, осуществляемого между одними и теми же источниками теплоты, имеющими постоянные, но разные температуры.

3) Обратимый цикл Карно имеет наибольший КПД по сравнению с любыми обратимыми или необратимыми циклами, в которых наибольшая и наименьшая температуры равны соответственно температуре горячего источника и температуре холодного источника цикла Карно.

23. Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей

Фундаментальными свойствами электрического заряда являются: существование двух видов заряда, его инвариантность, дискретность, аддитивность и подчинение закону сохранение заряда.

Закон сохранения заряда.

В изолированной системе суммарный заряд остается неизменным.

Закон Кулона: описывает взаимодействие двух точечных зарядов.

24. Напряженность-векторная величина, численно равная отношению суммы сил к величине этого заряда.

Напряженность поля точечного заряда, создаваемая зарядом на расстоянии r от него.

Принцип суперпозиции –напряженность поля, создаваемая системой зарядов равна геометрической сумме напряженностей этих полей.

25. Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности N_E.

Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду

Потенциал поля точечного заряда.

Принцип суперпозиции-потенциал поля, создаваемого системой зарядов равен алгебпроической сумме потенциалов поля, создаваемых каждым из зарядов.

27. Связь напряженности электрического поля с потенциалами в общем случае такова:

где   - скалярный и векторный потенциалы.

Напряженность и потенциал - различные характеристики одной и той же точки поля; следовательно, между ними должна существовать связь.

Рассматривая две точки с координатами (x, y, z) и (x+dx, y, z), между которыми перемещается заряд, можно сделать вывод, что напряженность как градиент потенциала имеет формулу:

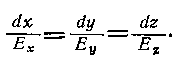
Величина, характеризующая быстроту изменения потенциала в направлении силовой линии, называется градиентом потенциала

Поверхность называется эквипотенциальной, если каждая её точка имеет одинаковый потенциал.

28. В проводнике, находящемся в электрическом поле устанавливаются равноместное распределение зарядов, при котором:. Напряжение электрического Поля внутри проводника равна 0, весь обьем проводника эквипотенциальный и заряды на проводнике всегда располагаются только на поверхности.

электростатическая защита. Если нужно уберечь от внешних электростатических полей какое-

либо устройство, его помещают в металлический ящик (или окружают металлической сеткой),

обнуляя напряжённость поля в пространстве вокруг устройства.

 C=qφ ,

где С – электроемкость уединенного проводника (Ф), φ – потенциал уединенного проводника (В), q – заряд уединенного проводника (Кл).

 C=qU ,

где С – электроемкость конденсатора (Ф), q – заряд конденсатора (Кл), U = φ₁ – φ₂ – разность потенциалов между обкладками конденсатора (напряжение на конденсаторе) (В).

Электроемкость плоского конденсатора равна

 C=ε0⋅ε⋅Sd ,

29. Дипо́ль — идеализированная система, служащая для приближённого описанияполя, создаваемого вообще говоря более сложными системами зарядов

Электрический дипольный момент — векторная физическая величина, характеризующая, наряду с суммарным зарядом (и реже используемыми высшими мультипольными моментами), электрические свойства Типы диэлектриков: неполярные (молекулы не обладают собственным дипольным моментом.),

Полярные(p=q*l) и ионные.

Поляризация-образование диполей, со направленных с внешним электрическим полем.

Диэлектрическая восприимчивость (или поляризуемость) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля

30. Энергия электростатического поля - это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора.

Энергия уединенного заряженного проводника

Плотность энергии электростатического поля.

Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема,