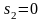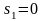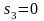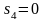- •Основные понятия исследования операций
- •Этапы проведения исследования операций
- •Математические модели операций Детермінована модель
- •Недетермінована модель
- •Классификация задач оптимизации
- •Теорема: Пусть х – выпуклое множество, x1, x2 , ….. , X k – произвольные точки из х. Тогда множество х содержит любую выпуклую линейную комбинацию этих точек.
- •Теорема: Пересечение произвольного числа выпуклых множества является выпуклым множеством. (Доказательство)
- •Задача линейного программирования. Экономическая интерпретация злп. Пропорциональность, аддитивность, неотрицательность Формы злп.
- •Экономическая интерпретация злп
- •Формы злп. Эквивалентность форм злп.
- •1.Формы злп
- •Эквивалентность различных форм злп
- •Базис матрицы а. Базисная матрица в. Базисное решение. Дбр. Нахождение базисного решения. Невырожденное и вырожденное дбр.
- •Доказательство того, что множество дбр системы конечно.
- •Доказательство
- •Принципиальная схема решения злп. Идея симплекс-метода.
- •Преобразованная задача (вывод). Особенности преобразованной задачи в частных случаях применения симплекс-метода (вырожденность, альтернативный оптимум, неограниченное мдр, неограниченная цф).
- •Способ перехода от одного базисного допустимого решения (бдр) к другому. Особые случаи, возникающие при переходе от одного дбр к другому.
- •Теорема (условие оптимальности). Для дбр операция замещения, при которой вводится в базис, изменяет значение цф на величину Если , то оптимально. (Доказательство)
- •Невырожденная и вырожденная злп. Отличия формулировок оптимальности дбр невырожденной и вырожденной злп.
- •5.5 Особливі випадки, що виникають при застосуванні симплекс-методу
- •5.5.1 Виродженість розв’язку
- •5.5.2 Необмежена множина допустимих розв’язків
- •5.5.3 Необмежена цільова функція
- •5.5.4 Альтернативний оптимум
- •Нахождение начального дбр (для стандартной, канонической и общей злп). Преобразованная задача для случая злп в стандартной форме.( "все ограничения типа '' ").
- •Искусственное начальное решение. Методы получения начального дбр.
- •6.2 Штучний початковий розв’язок
- •6.2 Штучний початковий розв’язок
- •6.3.2 Ознака відсутності др при реалізації -методу
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •6.2 Штучний початковий розв’язок
- •Искусственное начальное решение. Двухэтапный метод. Особые случаи, возникающие при применении метода. Штучний початковий розв’язок
- •Двохетапний метод
- •8.1 Двоїста задача
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •Доказательство утверждения (Следствие 2 теоремы двойственности 1):. Если цф пз не ограничена сверху, то двз не имеет допустимых решений.
- •Теорема 2 (о равенстве значений пары двойственных задач). Пусть прямая и двойственная задачи имеют решения и соответственно. Тогда выполняется равенство… . (Доказательство)
- •Получение решения задачи по решению двойственной задачи. Особенность симметричных задач
- •Соотношения дополняющей нежёсткости. Свойства взаимосвязанных пар переменных симметричной пары.
- •Алгоритм двойственности алгоритм двоїстості
- •Ценность ресурсов
- •8.5 Цінність ресурсів
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Недефицитный ресурс. (вывод соответствующих соотношений)
- •9.1 Аналіз зміни компонент вектора обмежень
- •9.1.1 Недефіцитний ресурс
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”). (вывод соответствующих соотношений).
- •9.1 Аналіз зміни компонент вектора обмежень
- •Дефіцитний ресурс
- •9.1.2.1 Обмеження виду “”
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”) (вывод соответствующих соотношений).
- •Постоптимальный анализ. Изменение коэффициентов цф - небазисная переменная (вывод соответствующих соотношений)
- •9.2.1 Небазисна змінна
- •9.2.1.1 Задача на максимум
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на максимум) (вывод соответствующих соотношений)
- •9.2.2 Базисна змінна
- •9.2.2.1 Задача на максимум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на минимум) (вывод соответствующих соотношений)
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов матрицы ограничений (вывод соответствующих соотношений) Аналіз зміни коефіцієнтів матриці обмежень
- •Двойственный симплекс-метод
- •8.6 Двоїстий симплекс-метод
- •Параметрическое программирование. Параметр в правой части
Способ перехода от одного базисного допустимого решения (бдр) к другому. Особые случаи, возникающие при переходе от одного дбр к другому.
Сначала рассмотрим конкретный пример.
Пусть имеем ЗЛП:
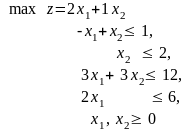
Приведем задачу к канонической форме
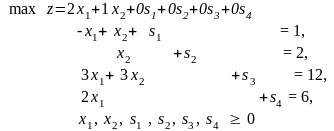
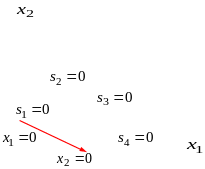
Нам необходимо найти какое-то ДБР. По определению ДБР:
ß – совокупность линейно-независимых векторов;
при ;
затем ;
если
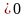 ,
то имеем ДБР с
,
то имеем ДБР с
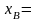 ,
иначе (имеем недопустимое БР) – все
нужно выполнить заново.
,
иначе (имеем недопустимое БР) – все
нужно выполнить заново.
Таким
образом, нужно найти базис, которому бы
ответствовало ДБР. Мы видим, что система
диагональная относительно переменных
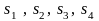 ,
и при этом правые части уравнений
неотрицательны. Если принять в качестве
базисных векторы, соответствующие этим
переменным, то получим, что
,
и при этом правые части уравнений
неотрицательны. Если принять в качестве
базисных векторы, соответствующие этим
переменным, то получим, что
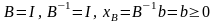 .
.
Точка
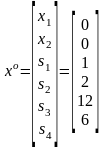 є ДБР (йому відповідає точка початку
координат
– точка A)..
є ДБР (йому відповідає точка початку
координат
– точка A)..

A B |
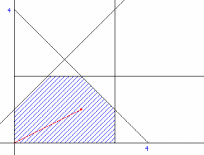
Запишемо систему обмежень відповідної перетвореної задачі:
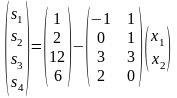
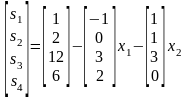
Нехай небазисна змінна почне зростати, приймаючи додатні значення, в той час, як інша небазисна змінна залишиться нульовою. Це означає, що ми починаємо рухатись по ребру AB. При збільшенні
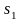 збільшується;
збільшується;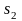 не
змінюється;
не
змінюється;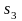 зменшується;
зменшується;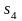 зменшується;
зменшується;
при
цьому змінна
першою обернеться в нуль (те, що буде
відбуватися з відповідною базисною
змінною, залежить від значення відповідної
компоненти вектора
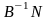 ).
Максимально допустиме значення збільшення
становить
).
Максимально допустиме значення збільшення
становить
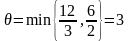
подальше збільшення приведе до того, що змінна тане від’ємною. А це означає, що розв’язок – недопустимий.
Отже,
якщо
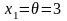 (ця змінна стане базисною), то
(ця змінна стане базисною), то
=0 (стане небазисною);
 ;
;
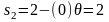 ;
;
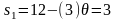 .
.
Це означає, що перейшли у інший ДБР (вершину В).
Теорема (условие оптимальности). Для дбр операция замещения, при которой вводится в базис, изменяет значение цф на величину Если , то оптимально. (Доказательство)
Докажем сначала I часть теоремы.
Как и ранее, будем предполагать, что переменные перенумерованы т.о., что первые столбцов матрицы составляют базис .
Обозначим
значение ЦФ в точке
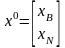
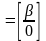 через
:
через
:
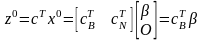
Операция замещения заключается в следующем:
начинаем
увеличивать небазисную переменную
,
при этом некоторые базисные переменные
уменьшаются и q-я
переменная первой достигает нулевого
значения, т.е. переменная
входит в базис, а переменная
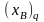 – выходит из него.
– выходит из него.

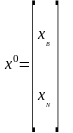
- первой обращается в ноль
начинаем увеличивать
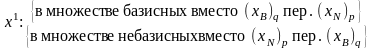
В результате операции замещения получаем новое ДБР , в котором:
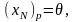 (вошедшая
из базиса переменная).
(вошедшая
из базиса переменная).
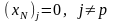 (остальные
небазисные переменные).
(остальные
небазисные переменные).
: 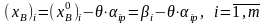 ,
и при этом
,
и при этом
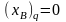 . (вышедшая
из базиса переменная);
. (вышедшая
из базиса переменная);
В векторной форме это записывается так (нумерация переменных сохраняется):
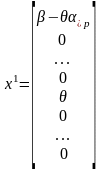 или
или
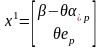 .
.
Знайдемо значення ЦФ в точці :
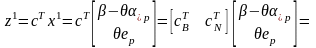
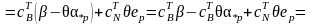
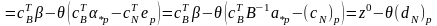 .
.
Отже, перша частина теореми доведена.
Докажем II часть теоремы.
Покажем теперь, что из условия следует оптимальность .
По
аналогии с вектором 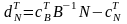
построим
вектор 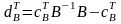 ,
,
где В – базисная матрица, соответствующая ДБР .
Тогда вектор
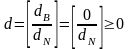 ,
т.к.
,
т.к.
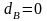 и
.
и
.
Можно записать, что
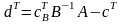 ,
,
действительно
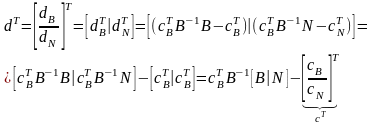
Итак
вектор
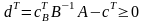 соответствует ДБР
.
соответствует ДБР
.
Пусть
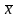 – произвольное
допустимое решение
исходной задачи (18) (не
обязательно
базисное),
т.е.
– произвольное
допустимое решение
исходной задачи (18) (не
обязательно
базисное),
т.е.
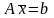 ,
,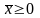 .
.
Очевидно,
что
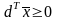 (скалярное произведение векторов с
неотрицательными компонентами).
(скалярное произведение векторов с
неотрицательными компонентами).
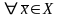 ,
,
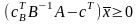 ,
,
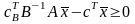
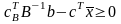
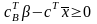
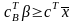
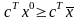
Отже оптимальний розв’язок.