
- •Основные понятия исследования операций
- •Этапы проведения исследования операций
- •Математические модели операций Детермінована модель
- •Недетермінована модель
- •Классификация задач оптимизации
- •Теорема: Пусть х – выпуклое множество, x1, x2 , ….. , X k – произвольные точки из х. Тогда множество х содержит любую выпуклую линейную комбинацию этих точек.
- •Теорема: Пересечение произвольного числа выпуклых множества является выпуклым множеством. (Доказательство)
- •Задача линейного программирования. Экономическая интерпретация злп. Пропорциональность, аддитивность, неотрицательность Формы злп.
- •Экономическая интерпретация злп
- •Формы злп. Эквивалентность форм злп.
- •1.Формы злп
- •Эквивалентность различных форм злп
- •Базис матрицы а. Базисная матрица в. Базисное решение. Дбр. Нахождение базисного решения. Невырожденное и вырожденное дбр.
- •Доказательство того, что множество дбр системы конечно.
- •Доказательство
- •Принципиальная схема решения злп. Идея симплекс-метода.
- •Преобразованная задача (вывод). Особенности преобразованной задачи в частных случаях применения симплекс-метода (вырожденность, альтернативный оптимум, неограниченное мдр, неограниченная цф).
- •Способ перехода от одного базисного допустимого решения (бдр) к другому. Особые случаи, возникающие при переходе от одного дбр к другому.
- •Теорема (условие оптимальности). Для дбр операция замещения, при которой вводится в базис, изменяет значение цф на величину Если , то оптимально. (Доказательство)
- •Невырожденная и вырожденная злп. Отличия формулировок оптимальности дбр невырожденной и вырожденной злп.
- •5.5 Особливі випадки, що виникають при застосуванні симплекс-методу
- •5.5.1 Виродженість розв’язку
- •5.5.2 Необмежена множина допустимих розв’язків
- •5.5.3 Необмежена цільова функція
- •5.5.4 Альтернативний оптимум
- •Нахождение начального дбр (для стандартной, канонической и общей злп). Преобразованная задача для случая злп в стандартной форме.( "все ограничения типа '' ").
- •Искусственное начальное решение. Методы получения начального дбр.
- •6.2 Штучний початковий розв’язок
- •6.2 Штучний початковий розв’язок
- •6.3.2 Ознака відсутності др при реалізації -методу
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •6.2 Штучний початковий розв’язок
- •Искусственное начальное решение. Двухэтапный метод. Особые случаи, возникающие при применении метода. Штучний початковий розв’язок
- •Двохетапний метод
- •8.1 Двоїста задача
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •Доказательство утверждения (Следствие 2 теоремы двойственности 1):. Если цф пз не ограничена сверху, то двз не имеет допустимых решений.
- •Теорема 2 (о равенстве значений пары двойственных задач). Пусть прямая и двойственная задачи имеют решения и соответственно. Тогда выполняется равенство… . (Доказательство)
- •Получение решения задачи по решению двойственной задачи. Особенность симметричных задач
- •Соотношения дополняющей нежёсткости. Свойства взаимосвязанных пар переменных симметричной пары.
- •Алгоритм двойственности алгоритм двоїстості
- •Ценность ресурсов
- •8.5 Цінність ресурсів
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Недефицитный ресурс. (вывод соответствующих соотношений)
- •9.1 Аналіз зміни компонент вектора обмежень
- •9.1.1 Недефіцитний ресурс
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”). (вывод соответствующих соотношений).
- •9.1 Аналіз зміни компонент вектора обмежень
- •Дефіцитний ресурс
- •9.1.2.1 Обмеження виду “”
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”) (вывод соответствующих соотношений).
- •Постоптимальный анализ. Изменение коэффициентов цф - небазисная переменная (вывод соответствующих соотношений)
- •9.2.1 Небазисна змінна
- •9.2.1.1 Задача на максимум
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на максимум) (вывод соответствующих соотношений)
- •9.2.2 Базисна змінна
- •9.2.2.1 Задача на максимум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на минимум) (вывод соответствующих соотношений)
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов матрицы ограничений (вывод соответствующих соотношений) Аналіз зміни коефіцієнтів матриці обмежень
- •Двойственный симплекс-метод
- •8.6 Двоїстий симплекс-метод
- •Параметрическое программирование. Параметр в правой части
Доказательство того, что множество дбр системы конечно.
Теорема. Множество ДБР системы конечно.
Доказательство
Т.к.
число различных подмножеств, состоящих
из
столбцов
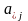 матрицы
конечно, то конечно и число линейно
независимых систем, составленных из
векторов
(это число ограничено величиной
матрицы
конечно, то конечно и число линейно
независимых систем, составленных из
векторов
(это число ограничено величиной
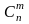 ).
).

Множество подмножеств по столбцов (его мощность )

Подмнож., сост. из
линейно независимых
столбцов (все возм. базисы)



Одному базису соотв. одно базисное решение!!!!


ДБР
Базисные решения
Теперь
покажем, что одной линейно независимой
системе векторов
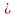 B
соответствует
единственное базисное решение, отсюда
будет следовать конечность множества
базисных решений.
B
соответствует
единственное базисное решение, отсюда
будет следовать конечность множества
базисных решений.
Пусть
вектора
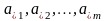 составляют базис B
(т.е.
они - линейно независимы). И пусть этому
базису соответствует два различных
базисных решения
составляют базис B
(т.е.
они - линейно независимы). И пусть этому
базису соответствует два различных
базисных решения
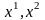 ,
т.е.
,
т.е.
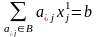 ,
,
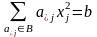 ,
,
Тогда справедливо:
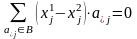 .
.
Т.к.
решения
и
различны, то, по крайней мере, один
коэффициент при
отличен от нуля, что противоречит условию
линейной независимости векторов
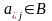 .
.
Итак, множество базисных решений конечно. . Ч.Т.Д.
Принципиальная схема решения злп. Идея симплекс-метода.
Согласно фундаментальной теореме вместо исследования бесконечного множества ДР, необходимо рассмотреть лишь конечное число ДБР. Таким образом, принципиальная схема решения ЗЛП такова:
Найти все ДБР.
Вычислить для каждого из них соответствующее значение ЦФ Z.
Сравнить и определить наилучшее.
НО!!!!
Но, в общем случае при больших значениях и m количество БР (и, значит и ДБР) может быть огромным (порядка ) и практическое осуществление перебора всех ДБР станет невозможным.
Эти трудности обусловлены тем, что указанная принципиальная схема связана с беспорядочным перебором ДБР, без учета, насколько новое проверяемое ДБР изменяет ЦФ Z и приближает ли оно нас к искомому оптимуму.
Число анализируемых ДБР можно резко сократить, если их перебор производить целенаправленно, добиваясь монотонного изменения ЦФ, т.е. чтобы каждое следующее ДБР было лучше предыдущего (или по крайней мере не хуже).
Основной метод решения ЗЛП – симплекс – метод - базируется на идее последовательного улучшения решения. Очевидно, что для реализации этой идеи метод должен включать три основных элемента:
Способ определения исходного ДБР.
Критерий, по которому можно определить оптимальность найденного решения или необходимость его дальнейшего улучшения.
Правило перехода к следующему “лучшему” ДБР.
Преобразованная задача (вывод). Особенности преобразованной задачи в частных случаях применения симплекс-метода (вырожденность, альтернативный оптимум, неограниченное мдр, неограниченная цф).
Рассмотрим ЗЛП в канонической форме:
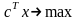 (1)
(1)
(2)
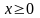 (3)
(3)
Пусть нам известно, что некоторый вектор х – ДБР системы (2).
Не теряя общности, предположим, что первые столбцов матрицы образуют базис данного ДБР.
Матрицу, составленную из векторов – столбцов, принадлежащих базису, мы условились называть базисной матрицей, по определению – базисная матрица невырожденна. |
Пусть
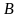 -
базисная матрица ДБР
(первые
столбцов матрицы
).
-
базисная матрица ДБР
(первые
столбцов матрицы
).
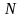 –
матрица,
составленная из остальных столбцов
матрицы
.
–
матрица,
составленная из остальных столбцов
матрицы
.
Тогда
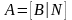 (4)
(4)
В
соответствии с представлением (4) разобьем
вектор
на подвекторы
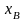 и
и
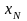 ,
т.е.
,
т.е.
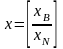 (5)
(5)
Переменные , соответствующие столбцам, вошедшим в базис, мы условились называть базисными переменными. Остальные переменные – небазисными.
где
– вектор базисных переменных,
– вектор небазисных переменных.
С учетом (4( и (5) систему (2) можно записать в виде:
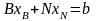 (6)
(6)
Так
как матрица
невырожденна, то она имеет обратную
матрицу
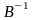 .
Домножим (6) слева на
.
.
Домножим (6) слева на
.
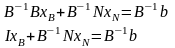
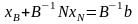
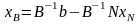 (7)
(7)
Система (7) эквивалентна системе (6), а, следовательно, и системе (2) .
?? Что означает эквивалентна??
Разобьем вектор с на подвекторы
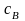 и
и
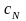 ,
в соответствии с разбиением матрицы
А:
,
в соответствии с разбиением матрицы
А:
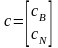 .
.
Тогда задачу (1) –(3) можно записать в виде:
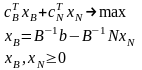
Подставим значение в ЦФ задачи:
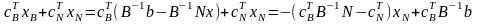
Тогда исходная задача может быть представлена в виде:
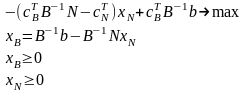
Получили так называемую преобразованную задачу. Обозначим
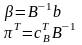
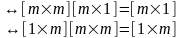
Можно записать преобразованную задачу следующим образом:
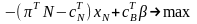 (8)
(8)
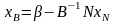 (9)
(9)
 (10)
(10)
