
- •Основные понятия исследования операций
- •Этапы проведения исследования операций
- •Математические модели операций Детермінована модель
- •Недетермінована модель
- •Классификация задач оптимизации
- •Теорема: Пусть х – выпуклое множество, x1, x2 , ….. , X k – произвольные точки из х. Тогда множество х содержит любую выпуклую линейную комбинацию этих точек.
- •Теорема: Пересечение произвольного числа выпуклых множества является выпуклым множеством. (Доказательство)
- •Задача линейного программирования. Экономическая интерпретация злп. Пропорциональность, аддитивность, неотрицательность Формы злп.
- •Экономическая интерпретация злп
- •Формы злп. Эквивалентность форм злп.
- •1.Формы злп
- •Эквивалентность различных форм злп
- •Базис матрицы а. Базисная матрица в. Базисное решение. Дбр. Нахождение базисного решения. Невырожденное и вырожденное дбр.
- •Доказательство того, что множество дбр системы конечно.
- •Доказательство
- •Принципиальная схема решения злп. Идея симплекс-метода.
- •Преобразованная задача (вывод). Особенности преобразованной задачи в частных случаях применения симплекс-метода (вырожденность, альтернативный оптимум, неограниченное мдр, неограниченная цф).
- •Способ перехода от одного базисного допустимого решения (бдр) к другому. Особые случаи, возникающие при переходе от одного дбр к другому.
- •Теорема (условие оптимальности). Для дбр операция замещения, при которой вводится в базис, изменяет значение цф на величину Если , то оптимально. (Доказательство)
- •Невырожденная и вырожденная злп. Отличия формулировок оптимальности дбр невырожденной и вырожденной злп.
- •5.5 Особливі випадки, що виникають при застосуванні симплекс-методу
- •5.5.1 Виродженість розв’язку
- •5.5.2 Необмежена множина допустимих розв’язків
- •5.5.3 Необмежена цільова функція
- •5.5.4 Альтернативний оптимум
- •Нахождение начального дбр (для стандартной, канонической и общей злп). Преобразованная задача для случая злп в стандартной форме.( "все ограничения типа '' ").
- •Искусственное начальное решение. Методы получения начального дбр.
- •6.2 Штучний початковий розв’язок
- •6.2 Штучний початковий розв’язок
- •6.3.2 Ознака відсутності др при реалізації -методу
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •6.2 Штучний початковий розв’язок
- •Искусственное начальное решение. Двухэтапный метод. Особые случаи, возникающие при применении метода. Штучний початковий розв’язок
- •Двохетапний метод
- •8.1 Двоїста задача
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •Доказательство утверждения (Следствие 2 теоремы двойственности 1):. Если цф пз не ограничена сверху, то двз не имеет допустимых решений.
- •Теорема 2 (о равенстве значений пары двойственных задач). Пусть прямая и двойственная задачи имеют решения и соответственно. Тогда выполняется равенство… . (Доказательство)
- •Получение решения задачи по решению двойственной задачи. Особенность симметричных задач
- •Соотношения дополняющей нежёсткости. Свойства взаимосвязанных пар переменных симметричной пары.
- •Алгоритм двойственности алгоритм двоїстості
- •Ценность ресурсов
- •8.5 Цінність ресурсів
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Недефицитный ресурс. (вывод соответствующих соотношений)
- •9.1 Аналіз зміни компонент вектора обмежень
- •9.1.1 Недефіцитний ресурс
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”). (вывод соответствующих соотношений).
- •9.1 Аналіз зміни компонент вектора обмежень
- •Дефіцитний ресурс
- •9.1.2.1 Обмеження виду “”
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”) (вывод соответствующих соотношений).
- •Постоптимальный анализ. Изменение коэффициентов цф - небазисная переменная (вывод соответствующих соотношений)
- •9.2.1 Небазисна змінна
- •9.2.1.1 Задача на максимум
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на максимум) (вывод соответствующих соотношений)
- •9.2.2 Базисна змінна
- •9.2.2.1 Задача на максимум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на минимум) (вывод соответствующих соотношений)
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов матрицы ограничений (вывод соответствующих соотношений) Аналіз зміни коефіцієнтів матриці обмежень
- •Двойственный симплекс-метод
- •8.6 Двоїстий симплекс-метод
- •Параметрическое программирование. Параметр в правой части
Теорема: Пусть х – выпуклое множество, x1, x2 , ….. , X k – произвольные точки из х. Тогда множество х содержит любую выпуклую линейную комбинацию этих точек.
Доведення:
Доведемо
за допомогою методу математичної
індукції (по числу точок
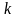 ).
).
Ситуація,
коли
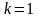 тривіальна.
тривіальна.
При
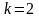 твердження теореми збігається з
визначенням опуклої множини.
твердження теореми збігається з
визначенням опуклої множини.
Нехай
будь-яка опукла лінійна комбінація
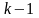 точок множини
належить даній множині.
точок множини
належить даній множині.
Розглянемо
точок
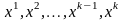 .
Їх лінійна опукла комбінація:
.
Їх лінійна опукла комбінація:
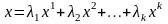 .
Якщо
.
Якщо
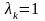 то
то
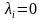 при
при
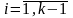 і
і
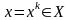
теорема справедлива.
теорема справедлива.
Нехай
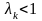 .
Тоді
.
Тоді
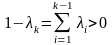 .
.
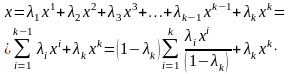
Числа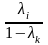 ,
- невід’ємні і їх сума дорівнює 1:
,
- невід’ємні і їх сума дорівнює 1:
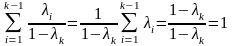
Отже,
вираз
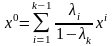 – опукла лінійна комбінація точок
– опукла лінійна комбінація точок
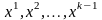 множини
.
За припущенням індукції
множини
.
За припущенням індукції
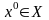 .
.
У
такому разі точка
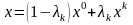 є опуклою лінійною комбінацією двох
точок з
,
отже,
.▀
є опуклою лінійною комбінацією двох
точок з
,
отже,
.▀
Гиперплоскость, полупространство, нормаль. Доказательство выпуклости гиперплоскости, полупространства
Теорема: Пересечение произвольного числа выпуклых множества является выпуклым множеством. (Доказательство)
Доказательство.
Рассмотрим
набор выпуклых множеств 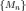 и
их пересечение:
и
их пересечение:
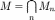 .
.
Рассмотрим
также две произвольные точки 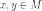 .
По определению пересечения множеств,
точки
.
По определению пересечения множеств,
точки  и
и  принадлежат
каждому множеству из набора
.
Так как каждое из этих множеств выпуклое,
то отрезок, соединяющий точки
и
,
также принадлежит каждому множеству
из
.
Отсюда, по свойству пересечения множеств,
следует, что этот отрезок принадлежит
и множеству
принадлежат
каждому множеству из набора
.
Так как каждое из этих множеств выпуклое,
то отрезок, соединяющий точки
и
,
также принадлежит каждому множеству
из
.
Отсюда, по свойству пересечения множеств,
следует, что этот отрезок принадлежит
и множеству 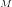 ,
а значит пересечение выпуклых множеств
действительно выпукло. Теорема доказана.
,
а значит пересечение выпуклых множеств
действительно выпукло. Теорема доказана.
Следует отметить, что пересечение двух выпуклых тел не всегда является выпуклым телом
Многогранное множество. Многогранник. Внутренняя, граничная точка, вершина множества. Свойства вершин (Условия того, что точка x* будет вершиной многогранного множества Х) . Вырожденная, невырожденная вершины.
Теорема ( о представлении многогранника): Множество точек многогранника совпадает с множеством любых выпуклых линейных комбинаций его вершин. (Доказательство)
Задача линейного программирования. Экономическая интерпретация злп. Пропорциональность, аддитивность, неотрицательность Формы злп.
Задача математического программирования вида:
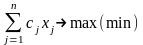 (1)
(1)
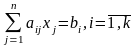 (2)
(2)
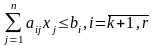 (3)
(3)
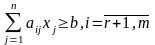 (4)
(4)
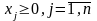 (5)
(5)
называется задачей линейного программирования (ЗЛП).
Ограничения неотрицательности могут накладываться не на все переменные, т.е. (5) могут иметь вид:
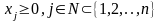
Экономическая интерпретация злп
Определить
такие объемы производства каждого вида
продукции
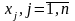 ,
при которых максимизируется доход (1) и
выполняются ограничения, накладываемые
на объёмы использования m
видов
ресурсов (2)-(4). [под ред. Дж.Моудера]
,
при которых максимизируется доход (1) и
выполняются ограничения, накладываемые
на объёмы использования m
видов
ресурсов (2)-(4). [под ред. Дж.Моудера]
Основными допущениями, принимаемыми при построении линейных моделей, является
1) пропорциональность
2) аддитивность
3) неотрицательность.
Пропорциональность означает, что
затраты ресурсов на некоторый вид продукции прямо пропорциональны его объему выпуска,
вклад этого вида продукции в ЦФ также прямо пропорционален его объему выпуска.
Аддитивность означает, что общая величина ресурса, используемого на производство всех видов продукции, равна сумме затрат этого ресурса на отдельные виды продукции. Аналогично интерпретируется и ЦФ.
Допущения о пропорциональности и аддитивности обеспечивают строгую линейность соответствующих функций.
Неотрицательность в большинстве практических случаев естественна, хотя обусловлена еще и удобствами аналитического представления.
