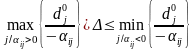- •Основные понятия исследования операций
- •Этапы проведения исследования операций
- •Математические модели операций Детермінована модель
- •Недетермінована модель
- •Классификация задач оптимизации
- •Теорема: Пусть х – выпуклое множество, x1, x2 , ….. , X k – произвольные точки из х. Тогда множество х содержит любую выпуклую линейную комбинацию этих точек.
- •Теорема: Пересечение произвольного числа выпуклых множества является выпуклым множеством. (Доказательство)
- •Задача линейного программирования. Экономическая интерпретация злп. Пропорциональность, аддитивность, неотрицательность Формы злп.
- •Экономическая интерпретация злп
- •Формы злп. Эквивалентность форм злп.
- •1.Формы злп
- •Эквивалентность различных форм злп
- •Базис матрицы а. Базисная матрица в. Базисное решение. Дбр. Нахождение базисного решения. Невырожденное и вырожденное дбр.
- •Доказательство того, что множество дбр системы конечно.
- •Доказательство
- •Принципиальная схема решения злп. Идея симплекс-метода.
- •Преобразованная задача (вывод). Особенности преобразованной задачи в частных случаях применения симплекс-метода (вырожденность, альтернативный оптимум, неограниченное мдр, неограниченная цф).
- •Способ перехода от одного базисного допустимого решения (бдр) к другому. Особые случаи, возникающие при переходе от одного дбр к другому.
- •Теорема (условие оптимальности). Для дбр операция замещения, при которой вводится в базис, изменяет значение цф на величину Если , то оптимально. (Доказательство)
- •Невырожденная и вырожденная злп. Отличия формулировок оптимальности дбр невырожденной и вырожденной злп.
- •5.5 Особливі випадки, що виникають при застосуванні симплекс-методу
- •5.5.1 Виродженість розв’язку
- •5.5.2 Необмежена множина допустимих розв’язків
- •5.5.3 Необмежена цільова функція
- •5.5.4 Альтернативний оптимум
- •Нахождение начального дбр (для стандартной, канонической и общей злп). Преобразованная задача для случая злп в стандартной форме.( "все ограничения типа '' ").
- •Искусственное начальное решение. Методы получения начального дбр.
- •6.2 Штучний початковий розв’язок
- •6.2 Штучний початковий розв’язок
- •6.3.2 Ознака відсутності др при реалізації -методу
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •6.2 Штучний початковий розв’язок
- •Искусственное начальное решение. Двухэтапный метод. Особые случаи, возникающие при применении метода. Штучний початковий розв’язок
- •Двохетапний метод
- •8.1 Двоїста задача
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •Доказательство утверждения (Следствие 2 теоремы двойственности 1):. Если цф пз не ограничена сверху, то двз не имеет допустимых решений.
- •Теорема 2 (о равенстве значений пары двойственных задач). Пусть прямая и двойственная задачи имеют решения и соответственно. Тогда выполняется равенство… . (Доказательство)
- •Получение решения задачи по решению двойственной задачи. Особенность симметричных задач
- •Соотношения дополняющей нежёсткости. Свойства взаимосвязанных пар переменных симметричной пары.
- •Алгоритм двойственности алгоритм двоїстості
- •Ценность ресурсов
- •8.5 Цінність ресурсів
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Недефицитный ресурс. (вывод соответствующих соотношений)
- •9.1 Аналіз зміни компонент вектора обмежень
- •9.1.1 Недефіцитний ресурс
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”). (вывод соответствующих соотношений).
- •9.1 Аналіз зміни компонент вектора обмежень
- •Дефіцитний ресурс
- •9.1.2.1 Обмеження виду “”
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”) (вывод соответствующих соотношений).
- •Постоптимальный анализ. Изменение коэффициентов цф - небазисная переменная (вывод соответствующих соотношений)
- •9.2.1 Небазисна змінна
- •9.2.1.1 Задача на максимум
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на максимум) (вывод соответствующих соотношений)
- •9.2.2 Базисна змінна
- •9.2.2.1 Задача на максимум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на минимум) (вывод соответствующих соотношений)
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов матрицы ограничений (вывод соответствующих соотношений) Аналіз зміни коефіцієнтів матриці обмежень
- •Двойственный симплекс-метод
- •8.6 Двоїстий симплекс-метод
- •Параметрическое программирование. Параметр в правой части
9.2.1 Небазисна змінна
Зміна коефіцієнта ЦФ небазисної змінної впливає на відносну оцінку тільки цієї змінної.
9.2.1.1 Задача на максимум
Нехай – оптимальний розв’язок, значить відповідний вектор відносних оцінок небазисних змінних
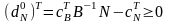 .
.
Відносна оцінка небазисної змінної :
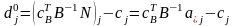 ,
,
величина не входить у вираз компонентів вектора , які відповідають іншим змінним.
Нехай коефіцієнт ЦФ при небазисній змінній прийняв значення
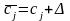 ,
,
тоді її нова відносна оцінка буде такою:
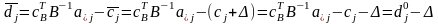
Розв’язок
залишиться оптимальним, якщо
 або
або
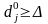 .
Отже, для небазисної змінної
діапазон
стійкості
в якому може змінюватися її коефіцієнт
ЦФ:
.
Отже, для небазисної змінної
діапазон
стійкості
в якому може змінюватися її коефіцієнт
ЦФ:
відносний
діапазон:
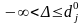 ,
,
абсолютний
діапазон: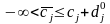 ,
,
де
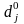 - відносна оцінка змінної
в оптимальному розв’язку.
- відносна оцінка змінної
в оптимальному розв’язку.
Якщо
 (
(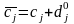 ),
то
стане одним з альтернативних оптимумів.
),
то
стане одним з альтернативних оптимумів.
9.2.1.2 Задача на мінімум
Нехай – оптимальний розв’язок, значить відповідний вектор відносних оцінок небазисних змінних
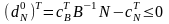 .
.
Нехай коефіцієнт ЦФ при небазисній змінній прийняв значення
тоді її нова відносна оцінка буде такою:
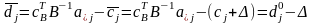
Розв’язок
залишиться оптимальним, якщо
 або
або
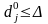 .
Отже, для небазисної змінної
діапазон
стійкості
в якому може змінюватися її коефіцієнт
ЦФ:
.
Отже, для небазисної змінної
діапазон
стійкості
в якому може змінюватися її коефіцієнт
ЦФ:
відносний
діапазон:
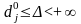 ,
,
абсолютний
діапазон:
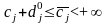 ,
,
де - відносна оцінка змінної в оптимальному розв’язку.
Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на максимум) (вывод соответствующих соотношений)
9.2.2 Базисна змінна
Нехай - оптимальний розв’язок ЗЛП.
9.2.2.1 Задача на максимум
В цьому випадку відповідний вектор відносних оцінок .
Варіювання коефіцієнта ЦФ базисної змінної впливає на відносні оцінки усіх небазисних змінних. Нехай змінюється коефіцієнт ЦФ -ї базисної змінної . В цьому випадку вектор коефіцієнтів ЦФ зміниться таким чином:
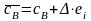 .
.
Тоді вектор відносних оцінок стане рівним
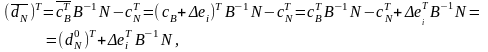
де
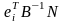 –
-й
рядок матриці
(коефіцієнти
-го
рядка симплекс-таблиці, що відповідають
небазисним змінним) .
–
-й
рядок матриці
(коефіцієнти
-го
рядка симплекс-таблиці, що відповідають
небазисним змінним) .
Відносна оцінка -ої небазисної змінної
 ,
,
де
 -
відносна оцінка
-ої
небазисної змінної в поточному
оптимальному розв’язку
.
-
відносна оцінка
-ої
небазисної змінної в поточному
оптимальному розв’язку
.
Для того, щоб розв’язок залишався оптимальним, повинна виконуватися умова
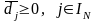 ,
,

 ,
,
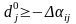 ,
.
,
.
Розділимо
-ту
нерівність на
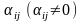 :
:
якщо
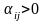 ,
то відповідна нерівність прийме вигляд
,
то відповідна нерівність прийме вигляд
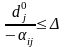 ,
,
якщо
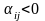 ,
то відповідна нерівність прийме вигляд
,
то відповідна нерівність прийме вигляд
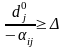 .
.
Отже, для базисної змінної діапазон стійкості, в якому може змінюватися коефіцієнт ЦФ , залишаючи поточний розв’язок оптимальним, задається виразом:
– відносний діапазон:
|
(6) |
(якщо
відсутні
чи
,
то
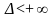 і
і
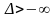 відповідно),
відповідно),
– абсолютний
діапазон:
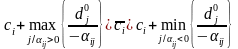 ,
,
Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на минимум) (вывод соответствующих соотношений)
Постоптимальний аналіз (аналіз моделей на чутливість) – це процес, який реалізується після того, як оптимальний розв’язок задачі отримано. У процесі такого аналізу виявляється чутливість оптимального розв’язку до певних змін початкової моделі. Іншими словами, аналізується вплив можливих змін початкових умов на отриманий раніше оптимальний розв’язок.
При такому аналізі завжди розглядається деяка сукупність оптимізаційних моделей. Це надає моделі певної динамічності, яка дозволяє проаналізувати вплив можливих змін початкових умов на отриманий раніше оптимальний розв’язок. Відсутність методів, що дозволяють виявити вплив можливих змін параметрів моделі на оптимальний розв’язок, може призвести до того, що отриманий (статичний) розв’язок застаріє ще до своєї реалізації.
У постоптмальному аналізі досліджуються три класи параметрів:
–– коефіцієнти вектора обмежень ;
–– коефіцієнти вектора ЦФ ;
–– коефіцієнти матриці .