Алгоритм двойственности алгоритм двоїстості
Крок
1.
Побудувати і розв’язати двоїсту задачу
оптимізації функції
,
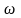отримати
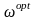і
.
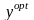Крок
2.
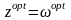(за теоремою 2).
Крок
3.
Визначення
значень компонент розв’язку
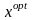(використовуючи СДН)
3.1. Цикл по змінних
Якщо змінна у оптимальному розв’язку базисна, то відповідну їй -у нерівність початкової системи прямої задачі замінити рівнянням-рівністю.
3.2. Після того, як частина рівнянь-нерівностей початкової системи прямої задачі заміниться рівностями, розв’язати цю систему рівнянь і знайти таким чином шукані значення змінних розв’язку .
Ценность ресурсов
8.5 Цінність ресурсів
Розглянемо ще одну економічну інтерпретацію значень двоїстих змінних.
Нехай i -е обмеження деякої ЗЛП має вигляд:
|
(32) |
.Після приведення до канонічної форми:
|
(33) |
.Нехай
– оптимальний розв’язок ЗЛП на максимум
(і оптимум не є альтернативним). Припустимо,
що змінна
,
що відповідає
-му
обмеженню, є небазисною. Оскільки
,
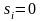то в точці оптимуму
початкове обмеження (32) виконується як
рівність:
.
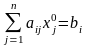Наступні міркування розіб'ємо на 4 пункти.
1.
Згідно теореми про умови оптимальності
в результаті операції заміщення ЦФ
змінюється на величину
,
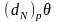де
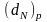– відносна оцінка змінної
,
що вводиться в базис;
– значення, яке приймає в новому ДБР, змінна ,
тобто
.
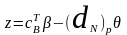З п.1 випливає п.2.
2.
Оскільки розв’язок
оптимальний, то відносна оцінка
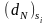залишкової змінної
додатна, і тому ЦФ буде зменшуватися
при зростанні залишкової змінної
і зростати при її зменшенні.
3. Подивимося на ситуацію з іншого боку. Нехай -а компонента вектора обмежень (об'єм -го ресурсу) збільшилася на 1 (рисунок 2), отже обмеження набуде вигляду:
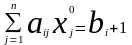
або після перестановки
.
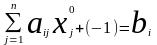Збільшення
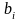еквівалентно зменшенню
(див. (33) ).
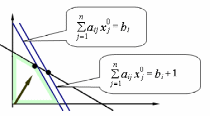
Рисунок 2
Тобто залишкова змінна повинна набути значення –1, щоб -е обмеження залишалося рівністю, і при цьому, згідно п.1., відносна оцінка змінної дає величину приросту ЦФ на одиницю збільшення елементу . Насправді, не може бути від’ємною (наприклад –1), тому, щоб залишити рівною 0 (небазисною), змінюються поточні значення базисних змінних, які, у свою чергу, повинні залишатися 0:
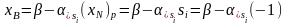
(з рисунку 2 – у нашому випадку при збільшенні правої частини рівняння змінна збільшується, а зменшується).
4. Раніше показали, що в точці оптимуму двоїсті змінні (що відповідають обмеженням виду «≤») збігаються з відносними оцінками відповідних залишкових змінних.
На підставі всіх цих 4-х пунктів робимо висновок: оскільки елемент зазвичай представляє об'єм -го ресурсу, то двоїста змінна (рівна відносній оцінці залишкової змінної) визначає відносну цінність одиниці додаткового ресурсу (цінність ресурсу).
Аналогічні міркування з точністю до знаку справедливі і для обмеження типу «≥» (в цьому випадку мова йде про надлишкові змінні).
Цей результат можна отримати і іншим, більш загальним способом (справедливим і для обмежень всіх типів). Згідно другої теореми двоїстості для оптимальних рішень пари взаємнодвоїстих задач справедливо:
.
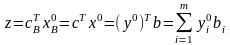Отже, швидкість зміни ЦФ при зміні в околі визначається формулою
,
,
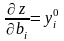тобто дорівнює двоїстій змінній.
Якщо змінна є базисною в точці оптимуму, то її відносна оцінка за визначенням дорівнює нулю – цінність відповідного ресурсу дорівнює нулю.
Дійсно,
якщо ресурс використаний не повністю:
,
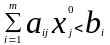то додаткова одиниця ресурсу не змінить
значення ЦФ.
Відмітимо два важливі моменти.
1) Не дивлячись на те, що цінність ресурсу вимірюється у вартісних одиницях, її не можна ототожнювати з дійсними цінами, за якими можлива закупівля відповідних ресурсів. Насправді мова йде про деяку міру, що має економічну природу і що кількісно характеризує цінність ресурсу щодо набутого оптимального значення ЦФ. (При зміні параметрів моделі відповідні економічні оцінки будуть змінюватися). Тому економісти віддають перевагу наступним термінам: тіньова ціна (shadow price); прихована ціна; оцінка ресурсу
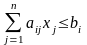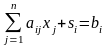