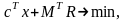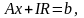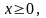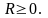- •Основные понятия исследования операций
- •Этапы проведения исследования операций
- •Математические модели операций Детермінована модель
- •Недетермінована модель
- •Классификация задач оптимизации
- •Теорема: Пусть х – выпуклое множество, x1, x2 , ….. , X k – произвольные точки из х. Тогда множество х содержит любую выпуклую линейную комбинацию этих точек.
- •Теорема: Пересечение произвольного числа выпуклых множества является выпуклым множеством. (Доказательство)
- •Задача линейного программирования. Экономическая интерпретация злп. Пропорциональность, аддитивность, неотрицательность Формы злп.
- •Экономическая интерпретация злп
- •Формы злп. Эквивалентность форм злп.
- •1.Формы злп
- •Эквивалентность различных форм злп
- •Базис матрицы а. Базисная матрица в. Базисное решение. Дбр. Нахождение базисного решения. Невырожденное и вырожденное дбр.
- •Доказательство того, что множество дбр системы конечно.
- •Доказательство
- •Принципиальная схема решения злп. Идея симплекс-метода.
- •Преобразованная задача (вывод). Особенности преобразованной задачи в частных случаях применения симплекс-метода (вырожденность, альтернативный оптимум, неограниченное мдр, неограниченная цф).
- •Способ перехода от одного базисного допустимого решения (бдр) к другому. Особые случаи, возникающие при переходе от одного дбр к другому.
- •Теорема (условие оптимальности). Для дбр операция замещения, при которой вводится в базис, изменяет значение цф на величину Если , то оптимально. (Доказательство)
- •Невырожденная и вырожденная злп. Отличия формулировок оптимальности дбр невырожденной и вырожденной злп.
- •5.5 Особливі випадки, що виникають при застосуванні симплекс-методу
- •5.5.1 Виродженість розв’язку
- •5.5.2 Необмежена множина допустимих розв’язків
- •5.5.3 Необмежена цільова функція
- •5.5.4 Альтернативний оптимум
- •Нахождение начального дбр (для стандартной, канонической и общей злп). Преобразованная задача для случая злп в стандартной форме.( "все ограничения типа '' ").
- •Искусственное начальное решение. Методы получения начального дбр.
- •6.2 Штучний початковий розв’язок
- •6.2 Штучний початковий розв’язок
- •6.3.2 Ознака відсутності др при реалізації -методу
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •6.2 Штучний початковий розв’язок
- •Искусственное начальное решение. Двухэтапный метод. Особые случаи, возникающие при применении метода. Штучний початковий розв’язок
- •Двохетапний метод
- •8.1 Двоїста задача
- •8.1.1 Правила побудови двоїстої задачі
- •8.1.2 Симетрична пара двоїстих задач
- •8.1.3 Несиметрична пара двоїстих задач
- •Доказательство утверждения (Следствие 2 теоремы двойственности 1):. Если цф пз не ограничена сверху, то двз не имеет допустимых решений.
- •Теорема 2 (о равенстве значений пары двойственных задач). Пусть прямая и двойственная задачи имеют решения и соответственно. Тогда выполняется равенство… . (Доказательство)
- •Получение решения задачи по решению двойственной задачи. Особенность симметричных задач
- •Соотношения дополняющей нежёсткости. Свойства взаимосвязанных пар переменных симметричной пары.
- •Алгоритм двойственности алгоритм двоїстості
- •Ценность ресурсов
- •8.5 Цінність ресурсів
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Недефицитный ресурс. (вывод соответствующих соотношений)
- •9.1 Аналіз зміни компонент вектора обмежень
- •9.1.1 Недефіцитний ресурс
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”). (вывод соответствующих соотношений).
- •9.1 Аналіз зміни компонент вектора обмежень
- •Дефіцитний ресурс
- •9.1.2.1 Обмеження виду “”
- •Постоптимальный анализ. Изменение компонент вектора ограничений. Дефицитный ресурс (ограничение типа “”) (вывод соответствующих соотношений).
- •Постоптимальный анализ. Изменение коэффициентов цф - небазисная переменная (вывод соответствующих соотношений)
- •9.2.1 Небазисна змінна
- •9.2.1.1 Задача на максимум
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на максимум) (вывод соответствующих соотношений)
- •9.2.2 Базисна змінна
- •9.2.2.1 Задача на максимум
- •Постоптимальный анализ. Изменение коэффициентов цф - базисная переменная (задача на минимум) (вывод соответствующих соотношений)
- •9.2.1.2 Задача на мінімум
- •Постоптимальный анализ. Изменение коэффициентов матрицы ограничений (вывод соответствующих соотношений) Аналіз зміни коефіцієнтів матриці обмежень
- •Двойственный симплекс-метод
- •8.6 Двоїстий симплекс-метод
- •Параметрическое программирование. Параметр в правой части
6.2 Штучний початковий розв’язок
Хай маємо ЗЛП в канонічній формі:
Ідея підходу припускає включення невід’ємних змінних в ліву частину кожного з рівнянь, що не містять «очевидних» початкових базисних змінних, тобто тих змінних, які входять тільки в одне рівняння з коефіцієнтом 1 (у симплекс-таблиці їй відповідає одиничний стовпець ).
Введемо в -е рівняння невід’ємну змінну :
,
,
…
,
…
.
Оскільки ці змінні не мають відношення до змісту поставленої задачі, вони отримали назву «штучних». Визначимо вектор штучних змінних:
.
Тоді система обмежень в матричній формі має вигляд: .
Штучні змінні забезпечують отримання початкового базису, тобто виконують ту ж роль, що і залишкові змінні (тобто вони використовуються тільки для отримання «стартової» точки).
Т.ч. початкове штучне рішення: .
Введення штучних змінних допустимо тільки в тому випадку, якщо відповідна схема обчислень змушуватиме ці змінні набувати нульових значень в кінцевому оптимальному розв’язку, забезпечуючи допустимість оптимуму. Для цього потрібно накласти «штраф» за використання штучних змінних. Розроблені два тісно зв'язаних між собою методи отримання початкового ДБР, в яких використовується «штрафування» штучних змінних:
–– -метод (або метод великих штрафів);
–– двохетапний метод.
6.3 - метод
В
цьому методі штучні змінні вводяться
в обмеження так, як це описано в п. 6.2.
При введенні ж до складу ЦФ кожній
змінній
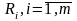 приписується штраф – достатньо великий
по модулю від’ємний коефіцієнт
приписується штраф – достатньо великий
по модулю від’ємний коефіцієнт
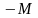 .
Такий спосіб введення штучних змінних
приводить до наступної лінійної моделі:
.
Такий спосіб введення штучних змінних
приводить до наступної лінійної моделі:
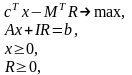
де
вектор
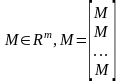 ,
,
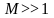 .
.
У
задачі
на мінімум
кожній змінній
приписується достатньо
великий додатній
коефіцієнт
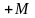 .
.
Розглянемо тепер, яким чином «нова» структура моделі автоматично приводить до того, що на кінцевій стадії процесу оптимізації змінні набувають нульового значення. Оскільки ми маємо справу із задачею на відшукання максимуму, а змінним у ЦФ приписаний великий по абсолютній величині коефіцієнт , то метод оптимізації, направлений на знаходження максимального значення ЦФ, приведе до того, що змінні в оптимальному розв’язку перетворяться у нуль.
Визначимо
компоненти перетвореної задачі,
відповідній початковому розв’язку, в
якому
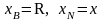 :
:
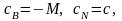
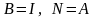 .
.
Числові значення ДБР (значення базисних змінних і відповідне значення ЦФ):
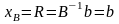 ,
,
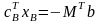 .
.
Компоненти вектора відносних оцінок небазисних змінних:
,
коефіцієнт при небазисній змінній :
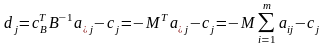
(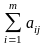 – сума коефіцієнтів вектор–стовпця
).
– сума коефіцієнтів вектор–стовпця
).
При застосуванні табличного симплекс-метода після отримання початкового ДБР необхідно перетворити - рядок так, щоб початковий розв’язок в явному вигляді фігурував в стовпці, що характеризує праві частини всіх рівнянь моделі. Для цього
з
відповідних обмежень задачі базисні
(у нашому випадку – штучні) змінні
виражаються через небазисні:
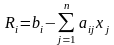 ,
;
,
;
вирази для штучних змінних підставляються в ЦФ :
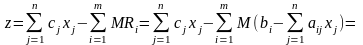
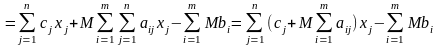 ,
,
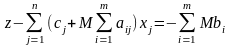 ,
,
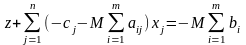 .
.
Якщо початкова задача – задача на мінімум, то при штучних змінних в - рядку усі коефіцієнти будуть мати протилежний знак: