§8 Эластичность функции
Будем рассматривать дифференцируемую
функцию
.
Как и ранее,
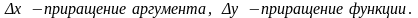Отношения
представляют собой относительные
приращения аргумента и функции
соответственно.
Величина
показывает, сколько процентов составляет
приращение ∆х относительно величины
самой переменной х. Аналогичную
характеристику дает и величина
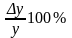
Отношение
показывает, сколько процентов составит
среднее ( на промежутке от х до х+∆х)
относительное приращение функции, если
относительное приращение аргумента
составляет 1%.
Предел
называют
эластичностью функции
по её аргументу в точке х (читают:
«Эластичность игрек относительно
икс»).Эластичность функции по её
аргументу показывает, на сколько
процентов изменится значение функции
при увеличении аргумента в точке х
на 1%.
Таким образом, эластичность у по её аргументу х можно вычислить по формуле
Пример1
Рассчитайте эластичность функции
при
х = 1
х = 1,
Это означает, что при увеличении х на 1% у уменьшится на 1%
При х = 2,
,
т.е. при увеличении х на 1% у
уменьшится на 7%
Пример2
Известно, что спрос на товар зависит
от доходов потребителей. При увеличении
доходов потребители могут переключится
на товар лучшего качества или на
какой-либо заменитель товара. Таким
образом, спрос q
зависит от дохода r,
q=q(r).
Эластичность спроса относительно
дохода
показывает, на сколько процентов
увеличится спрос при увеличении дохода
на 1%.
Например, если q(r)=50-0,1r,
то
Так, при доходе r =10
получаем ,
,
а при увеличении дохода на 10% спрос
уменьшится на
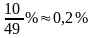
Замечание1
Спрос q на товар
зависит от цены р, q=q(p)
, причем обычно спрос понижается при
увеличении цены и тогда
.
Поэтому эластичностью спроса q
относительно цены р называют
величину
.
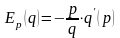Она показывает, на сколько процентов
уменьшится спрос при увеличении цены
на 1%.
Замечание1
Спрос называют эластичным, если
.
При
спрос называют нейтральным.
Если
,
то говорят, что спрос неэластичен.
Для функции спроса q (p)=20-3p найдем эластичность спроса по цене при р=2.
Можно сделать вывод, что при повышении
первоначальной цены на 1% спрос уменьшиться
на
Пример3
Зависимость спроса q
и предложения s от
цены р задается функциями
Выясним,
что произойдет в условиях равновесия
рынка при увеличении цены на 1%.
Условия равновесия означают, что спрос
и предложения уравновешены, q
(p)=s(p),
т.е.
откуда р=5. Эластичность спроса по
цене
При р=5 получаем
.
Следовательно, при увеличении цены на
1% СПРОС УМЕНЬШИТСЯ ПРИБЛИЗИТЕЛЬНО
НА 0,89%
Эластичность предложения по цене
При р=5 получаем
.
Значит, при увеличении цены на 1%
предложение увеличится приблизительно
на 0,11%.
*Для функции спроса
в зависимости от цены х найти
эластичность спроса по цене
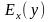в точках х=1, х=4, х=8, х=10.
*Для функции предложения у=8х+3 в зависимости от цены х найти эластичность предложения по цене в каждой из точек х=2, х=3, х=5, х=10.
* В предложенных выше заданиях выяснить, является ли спрос или предложение эластичным, нейтральным или неэластичным в каждом из рассмотренных случаев.