§6 Непрерывность функции. Точки разрыва. Асимптоты графика функции
2
1
1
Рассмотрим функцию
Функция определена в точке
=1.
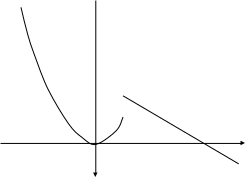
По виду графика замечаем, что если точка х приближается к 1, оставаясь меньше 1, т.е. слева, то соответствующие значения функции всё меньше отличаются от 1. Говорят, что 1 – есть предел функции f(x) слева в точке =1.
По графику при приближении х к 1 справа, т.е. когда х принимает значения больше 1, соответствующие значения функции как угодно близко приближаются к 2. Говорят, что 2 – предел функции справа в точке =1.
Записывают,
и
Такие пределы называются односторонними.
Теорема.
Функция у=f(x) имеет предел в точке тогда и только тогда, когда в этой точке существует правый и левый пределы и они равны. В этом случае их общее значение и является пределом функции f(x) в точке .
Пример.
Найти предел функции в точке
=0.
Согласно теореме, функция f(x) в точке =0 предела не имеет.
Функция у=f(x) называется непрерывной в точке , если:
1)функция определена в этой точке;
2)в некоторой окрестности точки существует предел функции в точке , который совпадает со значением функции в этой точке.
Т.е.
При невыполнении одного из этих условий функция терпит разрыв в точке .
Рассмотрим классификацию точек разрыва.
Точка называется точкой разрыва I рода функции f(x) , если в этой точке существуют конечные пределы справа и слева в точке , не равные друг другу.
Точка называется точкой разрыва II рода функции f(x) , если в этой точке правый или левый пределы не существуют или являются бесконечными.
Пример.
Найдите точки разрыва функции f(x) и выясните характер этих точек.
а)
Функция определена на всей числовой прямой. Найдем односторонние пределы в точке =1
,
Односторонние пределы существуют, конечны, но не равны друг другу, следовательно =1 – точка разрыва I рода.
б) f(x)=
Функция определена всюду, кроме точки = -1, значит = -1 – точка разрыва. Установим какого рода.
,
Значит, = -1 – точка разрыва II рода.
в)
Функция определена всюду, кроме точки = 1, значит = 1 – точка разрыва. Установим какого рода.
,
Поскольку односторонние пределы в точке 1 бесконечны, то = 1 – точка разрыва II рода.
Исследуем функцию в окрестности точки
=
0
,
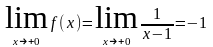
Односторонние пределы существуют, конечны, равны друг другу, проверим значение функции в точке =0
f(
)=f(0)=
Значение функции совпадает с односторонними пределами, следовательно, в точке =0 разрыва нет.
УПРАЖНЕНИЕ:
Определите точки разрыва функции, их характер и постройте схематичный график функции
у =
у =
у =
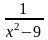
у =
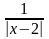
у =
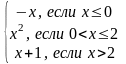
у =
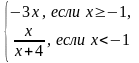
у =
у = 3
у =
у =
у=
Асимптоты графика функции
Прямая L называется асимптотой кривой, заданной уравнением y = f(x), если расстояние между точками кривой и прямой стремится к нулю с удалением точки на кривой от начала координат.
Существуют вертикальные, наклонные или горизонтальные асимптоты.
х = а – вертикальная асимптота, если
- точка разрыва II
рода
- наклонная асимптота, если существуют
конечные k и b,
которые вычисляются по формулам:
Если
,
то
-
горизонтальная асимптота.
Пример
Найдите асимптоты графика функции
D(y)
= (
Тогда =0 – точка разрыва. Установим характер разрыва.
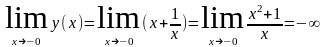
Установили, что =0 – точка разрыва II рода, х = 0 – вертикальная асимптота
Проверим, имеет ли график наклонные асимптоты вида
Получили,
что
=1х+0,
т.е. у = х – наклонная асимптота.
УПРАЖНЕНИЕ:
Найдите асимптоты кривых
