4 Определение амплитуды установившихся колебаний. Расчет траектории движения центра масс двигателя

Исходные данные: скорость вращения ротора n=214 об/мин, амплитуда возмущающей нагрузки P=2100 Н. В случае равномерного вращения (φ=Θt) нагрузку можно разложить на составляющие P_i (i – номер обобщенной координаты, в направлении которой прикладывается составляющая):

,

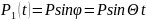
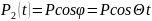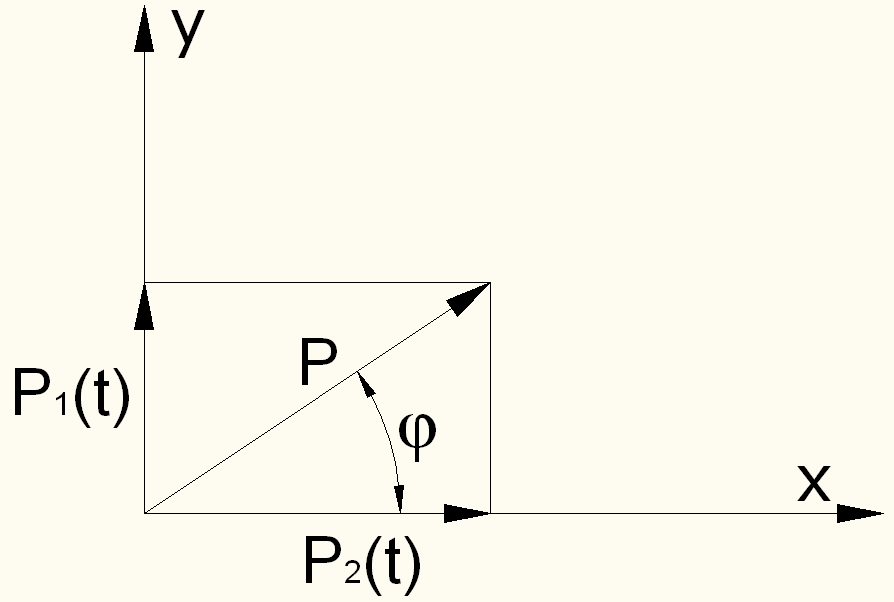
Рисунок 11 - Разложение нагрузки Р

Поскольку система линейна, можно использовать принцип суперпозиции: рассчитать отдельно на силы P₁(t) и P₂(t), а затем сложить результаты. Сформируем векторы амплитуд гармонической нагрузки косинусоидального (Pc) и синусоидального (Ps) характера:

, .

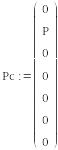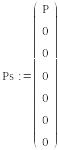Константа Р в данных векторах занимает место, соответствующее той обобщенной координате, по направлению которой приложена гармоническая нагрузка. Например, нагрузка P₂(t), имеющая косинусоидальный характер, приложена в направлении обобщенной координаты q₂ , поэтому амплитуду Р этой нагрузки размещаем на месте второго компонента вектора Р_c.

Амплитуды A_c и A_s установившихся колебаний от воздействия косинусоидальной и синусоидальной нагрузки определяются из векторных уравнений:

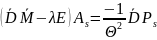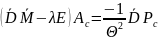, , (5.2)

в которых - матрица относительных податливостей, 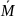– матрица относительных масс (в данном случае численно совпадает с М), Е - единичная матрица, q - круговая частота нагрузки, А_s и А_с – искомые векторы амплитуд колебаний соответственно от синусоидальной и косинусоидальной составляющих нагрузки. Размерность всех векторов и матриц совпадает с числом степеней свободы механической системы.

Параметр l определим по формуле:

(5.3)

Получим λ=2,599*10⁴. Выразим из уравнений 5.2 амплитуды A_c и A_s:

, (5.4)

Результаты вычислений (в м):

.

Вектор амплитуд А от суммарного действия составляющих P₁(t) и P₂(t):

(5.5)

Для данной задачи он равен (в м):

Вектор узловых перемещений по направлениям обобщенных координат:

(5.6)

Траекторию движения центра масс электродвигателя рассчитаем без учета его эксцентриситета относительно оси вращения ротора, т.е. фактически рассчитывается динамическое перемещение оси вращения. Результаты построений представлены на рисунке 12. Из построенного графика видим, что траектория представляет собой эллипс.

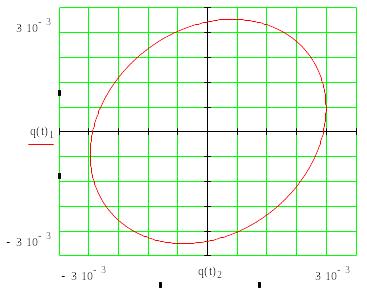
Рисунок 12 – Траектория движения центра масс электродвигателя (в м)

5 Построение эпюры изгибающих моментов в амплитудном состоянии

Для построения динамической эпюры изгибающих моментов необходимо найти значения сил инерции в амплитудном состоянии по направлениям обобщенных координат q₁, q₂,…, q₇. Векторы сил инерции Ф_s, Ф_с, возникающих соответственно от синусоидальной и косинусоидальной составляющих гармонической нагрузки, определим из уравнений:

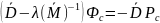, (6.1)

Решение данных уравнений:

, (6.2)

Результаты вычислений (в Н):

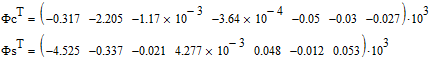
Амплитудные значения изгибающих моментов определяют из расчета рамы на суммарное действие вычисленных сил инерции и амплитудных значений составляющих гармонической нагрузки. Эпюру моментов целесообразно построить, используя единичные эпюры моментов :

, ,

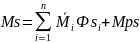в которых Фs_i – i-й компонент вектора Фs, Мps – эпюра статических моментов от действия амплитуды «синусоидальной» силы P₁(t), n – число степеней свободы системы. Обозначения во втором уравнении имеют аналогичный смысл. Очевидно, , .

Для представления эпюр в численном виде на раме необходимо отметить ряд сечений. Количество сечений n_s должно быть таким, чтобы любая единичная или грузовая эпюра однозначно представлялась соответствующим числовым вектором. Если в жестком узле соединяются три стержня, то рассматривают три сечения, примыкающие к узлу. Данную раму я счел целесообразным рассечь 11-ю сечениями (n_s=11) (рисунок 13).

Рисунок 13 – Расположение и нумерация сечений

Необходимо также назначить правило знаков, поскольку обычно на эпюрах моментов в рамах знаки не ставятся. Например, в рассматриваемой задаче за положительные ординаты приняты следующие: на горизонтальном стержне – отложенные сверху, на вертикальном стержне – справа. В таблице 2 приведены значения ординат единичных и грузовых эпюр в намеченных сечениях.

Таблица 2 – Значения единичных моментов , а также Mps и Mpc в сечениях рамы

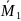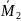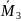Сечения	, м	, м	, м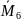	, м	, м	, м	, м	Mpc, кН*м	Mps, кН*м
1	0	0	0	0	0	0	0	0	0
2	1,15	0	0	0	0	0	0	0	2,415
3	2,3	0	1,15	0	0	0	0	0	4,83
4	2,3	0	1,15	0	-2,3	0	-4,6	0	4,83
5	1,15	-2,3	0,575	-0,575	-3,45	-1,15	-4,6	-4,83	2,415
6	0	-4,6	0	0	-4,6	-2,3	-4,6	-9,66	0
7	0	0	0	0	2,3	0	4,6	0	0
8	0	0	0	0	0	0	2,3	0	0
9	0	0	0	0	0	0	0	0	0
10	0	-2,3	0	0	-2,3	-2,3	-2,3	-4,83	0
11	0	0	0	0	0	0	0	0	0

Значения векторов Ms и Mc (в Н*м):

Графически изобразим данные векторы в виде эпюр на рисунке 14.

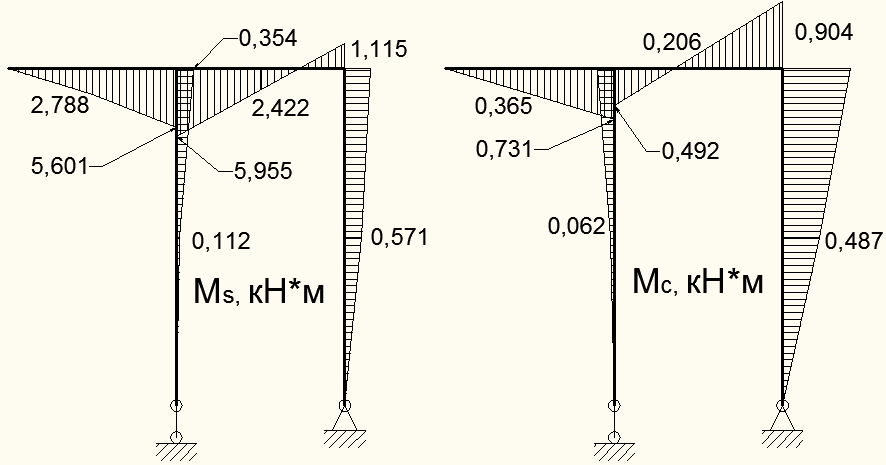
Рисунок 14 - Амплитудные эпюры моментов от составляющих

вибрационной нагрузки P₁(t) и P₂(t)

Эпюра динамических моментов изменяется во времени по формуле . Максимальные по модулю значения динамических моментов определяются выражением:

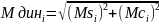, i=1,2…n_s

и в данном случае составят (в Нм):

Итак, максимальный изгибающий момент в раме, обусловленный действием гармонической нагрузки, в условиях стационарных колебаний:

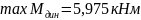
Он возникает в сечении 4 (узел с сосредоточенной массой m₃).

Максимальные динамические напряжения в узле:

Кроме динамической нагрузки, учтем силу тяжести электродвигателя Q=15 кН в виде вектора

,

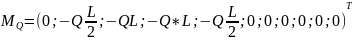Тогда суммарный изгибающий момент составит 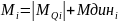. Своего максимального значения он, также как и М_дин, достигнет в 4-м сечении: Mmax=40,475 кН*м.

Максимальные суммарные напряжения:

.

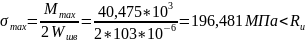Аналогично при неработающем электродвигателе:

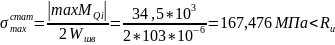
Различие между последними величинами составляет 17,3 %.