Министерство образования Российской Федерации

Федеральное государственное бюджетное

образовательное учреждение высшего профессионального образования

Алтайский государственный технический университет

им. И.И. Ползунова

Кафедра "Прикладная механика"

УДК 534.1 (075.8) Курсовой проект защищен

с оценкой _______________

Руководитель доцент,

к.т.н. ________В.Г.Бусыгин

Динамический расчет массивной плоской рамы Пояснительная записка к курсовому проекту по дисциплине

«Аналитическая динамика и теория колебаний»

КП 150301.83.000ПЗ

Студент группы ДПМ-81__________________О. Ю. Матвиенко

Барнаул 2012

1 Техническое задание

Дана массивная стальная плоская рама с установленным на ней электродвигателем весом Q=15 кН (рисунок 1). Поперечные сечения всех стержней рамы одинаковы и выполнены в виде составного сечения из двух швеллеров. Вследствие вращения неуравновешенного ротора электродвигателя со скоростью n=214 об/мин возникает центробежная сила величиной Р=2,1 кН, которая вызывает колебания рамы.

Рисунок 1 - Исследуемая плоская рама

Требуется:

1. подобрать номер швеллера из условия статической прочности;

2. используя упрощенную расчетную схему с двумя степенями свободы, определить собственные частоты колебаний ω₁ и ω₂, формы колебаний, пренебрегая массой стержней рамы;

3. рассчитать спектр собственных колебаний рамы по уточненной схеме, приближенно учитывающей массу стержней рамы;

4. рассматривая стационарный режим колебаний, определить амплитуду установившихся колебаний массы электродвигателя и рассчитать траекторию движения центра масс электродвигателя;

5. построить эпюру амплитудных значений изгибающих моментов, возникающих в раме от действия заданной вибрационной нагрузки при стационарном режиме колебаний;

6. вычислить максимальные динамические напряжения в сечениях рамы (с учетом собственного веса двигателя) и сравнить их с расчетным сопротивлением материала;

7. сравнить значения максимальных динамических напряжений со значениями, полученными из статического расчета и сделать заключение о прочности рамы.

Расчетное сопротивление стали изгибу принять равным R_u= 210 МПа, модуль упругости стали Е = 200 ГПа, длина L=2,3 м.

Оглавление

Динамический расчет 1

Пояснительная записка к курсовому проекту по дисциплине 1

1 Техническое задание 2

2 Определение спектра собственных колебаний по упрощенной схеме 5

2.1 Выбор номера швеллера 5

2.2 Вычисление параметров собственных колебаний 6

3 Расчет спектра собственных колебаний по уточненной схеме 9

4 Определение амплитуды установившихся колебаний. Расчет траектории движения центра масс двигателя 14

5 Построение эпюры изгибающих моментов в амплитудном состоянии 17

7 Список литературы 22

Приложение 1 23

2 Определение спектра собственных колебаний по упрощенной схеме

2.1 Выбор номера швеллера

Расчет спектра собственных колебаний рамы можно выполнить, если известна изгибная жесткость стержней, из которых состоит данная рама. В свою очередь, изгибная жесткость зависит от размеров поперечного сечения стержней (в данном случае оно представляет собой два швеллера, повернутые друг к другу длинными сторонами). Для нахождения оптимальных параметров сечения проведем статический расчет исходной рамы на прочность от действия суммарной силы Q + P.

На основании знаний, полученных из курса “Сопротивление материалов”, построим эпюру изгибающих моментов.

Рисунок 2 - Эпюра изгибающих моментов

Значение максимального изгибающего момента: . Условие статической прочности:

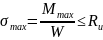(3.1)

где σ_max – максимальное нормальное напряжение в поперечном сечении, M_max- максимальный изгибающий момент, W – момент сопротивления сечения, R_и – сопротивление изгибу.

Тогда искомый момент сопротивления сечения:

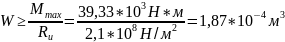
Поскольку поперечное сечение состоит из двух швеллеров, то:

Выбираем из ГОСТ 8240-97 швеллер №16аП со следующими параметрами: площадь поперечного сечения F=19,5 см², погонная масса , момент сопротивления W_шв=103 см³, момент инерции I_xш=827см⁴.

Изгибная жесткость сечения:

Масса двигателя: