Следствия из уравнений Гиббса-Дюгема

Следствие 1 (для бинарной системы)

Это соотношение позволяет проверять экспериментальные результаты. Знак минуса показывает, что всегда возрастание ПМВ одного компонента будет сопровождаться уменьшением ПМВ другого.

Следствие 2 (для бинарной системы)

Можно вычислить изменение ПМВ одного из компонентов при переходе от одной концентрации к другой, если известно изменение ПМВ второго компонента.

Следствие 3

Изменение экстенсивного свойства системы можно вычислить через изменение ПМВ компонентов системы.

Следствие 4

Для ПМВ остаются справедливыми все термодинамические соотношения, применяемые для чистых веществ.

Пример 1.

Задание. Вычислить удельную теплоемкость водного раствора, содержащего 37,5 % (масс) H₂SO₄. Парциальные молярные теплоемкости при 298 К для H₂SO₄ и для Н₂О соответственно равны 61,7 и 77,8 Дж/моль К.

Решение.

1. Перейдем от массовых долей к мольным. Для этого выделим мысленно 100 г раствора и воспользуемся формулой (1.5). тогда для серной кислоты:

Для воды:

2. 3. Масса 1 моль раствора:

Удельная теплоемкость раствора:

Пример 2.

Задание. Вычислить теплоту растворения 1 моль HCl в 10 молях Н₂О, если изменения парциальных молярных энтальпий составляет для Н₂О -11,38 кДж/моль, а для HCl -4,18 кДж/моль.

Решение.

Найдем мольные доли соляной кислоты и воды.

Тогда для 1 моль раствора:

кДж/моль

для 11 моль раствора:

кДж.

Пример 3.

Задание. Рассчитать изменение парциальной молярной энтальпии уксусной кислоты, если при смешивании 79,4 г уксусной кислоты и 20,6 г воды выделяется 805 Дж теплоты. Изменение парциальной молярной энтальпии воды в этом растворе составляет –133,9 Дж/моль.

Решение.

Общий тепловой эффект процесса определяется уравнением:

пример 4.

Задание. Определить для системы ртуть (индекс 1)- таллий (индекс 2), в которой молярная доля таллия составляет 0,25, парциальную молярную энтальпию, а также изменение энергии Гиббса, энтальпии и энтропии при образовании 1 кг раствора данной концентрации при температуре 298 К. Парциальная молярная энергия Гиббса равна:  Дж/моль;  Дж/моль. Парциальные молярные энтропии:  Дж/мольК;  Дж/мольК

Решение.

Вычисляем изменение энергии Гиббса для образования одного моля раствора по уравнению:

Вычисляем молярную массу раствора по уравнению:

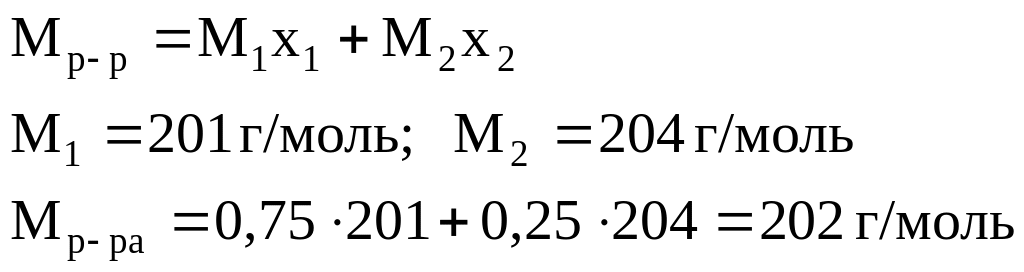
Вычисляем изменение энергии Гиббса при образовании 1 кг раствора по уравнению:

Вычисляем изменение энтропии при образовании одного моля раствора:

вычисляем изменение энтропии при образовании 1 кг раствора:

Дж/кг К

Вычисляем изменение энтальпии при образовании 1 кг раствора по уравнению:

Вычисляем парциальные молярные энтальпии обоих компонентов по уравнениям:

Относительные пм свойства

Эта величина представляет собой разность ПМВ компонента в данном растворе и свойств того же компонента в стандартном состоянии или в чистом виде.

По физическому смыслу относительная парциальная мольная величина представляет собой изменение молярной величины при растворении одного моля компонента в растворе данной концентрации. В связи с этим называют просто парциальной мольной величиной растворения компонента (например, – парциальная молярная теплота растворения).

Отметим, что при растворении 1 моля вещества в бесконечно большом количестве раствора тепловой эффект иногда называют дифференциальной теплотой растворения в отличие от интегральной теплоты, которая представляет собой тепловой эффект при растворении 1 моля вещества в таком количестве растворителя, которое требуется для создания данной концентрации. Для относительных парциальных мольных величин справедливы все уравнения, выведенные для чистых веществ, если заменить в них мольные величины парциальными мольными величинами.

Сведения о зависимости парциальных мольных величин от концентрации представляют первостепенный интерес для термодинамики растворов. Наименьшее количество экспериментальных данных требуется для термодинамической характеристики бинарных растворов. Но даже для этих систем зависимость Z от концентрации приобретает общность только в случае идеальных или бесконечно разбавленных растворов. Математический анализ уравнения Гиббса-Дюгема показывает, что существует небольшое число видов зависимости парциальных мольных величин от концентрации.

Проще всего эти зависимости обнаруживаются в так называемых идеальных растворах.