Структура управления оптимального по быстродействию, определение моментов переключения.
Объект управления описывается системой
(1)
На управление наложены ограничения:
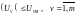(2)
Требуется найти допустимое управление , которое за минимально возможное время Т переводит объект из заданного начального состояния в конечное состояние Х(Т)=ХТ.
Оптимизируемый функционал, в задача максимального быстродействия имеет вид
(3)
т.е. при оптимизации системы управления по быстродействию в интегральном функционале берется .
Поэтому функция Гамильтона в этом случае
(4)
Так как , максимум Н реализуется одновременно с максимумом функции
(5)
Согласно основной теореме принципа максимума в задаче, в которой T не фиксировано, должно выполняться условие
(6)
Таким образом, для оптимальности по быстродействию необходимо:
1) существование ненулевой, непрерывной векторной функции составляющие которой удовлетворяют системе
(7)
2) чтобы функция при каждом значении достигала максимума по ;
3) чтобы при выполнялось соотношение (6).
Основная
задача определения оптимальных по
быстродействию алгоритмов управления
в разомкнутых системах состоит в
нахождении моментов переключения реле
.
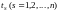так как на основании теоремы об "
"
интервалах управление является релейным
с числом интервалов не более
,
на которых
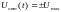и имеет место
переключений реле.
Определение
моментов переключения
в общем случае является сложной задачей.
Моменты переключения зависят от следующих факторов:
1)
от векторов начального и конечного
состояния объекта
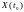и
;
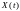2)
от наличия ограничений координат
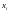вектора состояния;
3) от величины допустимого управления
4) от параметров и характеристик объекта;
5) от наличия возмущающего воздействия.
Рассмотрим способ вычисления моментов переключения на примере одномерного линейного объекта с неизменными во времени параметрами при отсутствии ограничений на базовые координаты и отсутствии возмущений.
Пусть дифференциальное уравнение объекта управления имеет вид
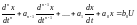(8)
где
,
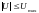а корни характеристического уравнения
являются вещественными и отрицательными.
Требуется
за минимальное время перевести объект
из заданного начального состояния
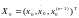в заданное конечное состояние
.
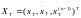Согласно
теории об "
"
интервалах оптимальное управление для
объекта, описываемого уравнением (8)
будет содержать
чередующихся по знаку интервалов
управления. Для определения моментов
переключения
применим способ стыкования управляемой
координаты
и всех её производных до
включительно. Этот способ основан на
том, что состояние системы в конце
каждого интервала играет роль начальных
условий для движения на следующем
интервале. Когда объект описывается
уравнением типа (8), координата
и ее производные до
-гo порядка при изменении знака управления
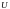остаются непрерывными. В этом случае
стыкование в моменты переключения
управления сводятся к приравниванию
значений координаты
и ее производных, полученных из решений
уравнения (8) на двух соседних интервалах.
Если объект описывается уравнением, которое содержит в правой части производные от управляющего воздействия, некоторые производные от координаты Х претерпевают разрыв в моменты переключения. Тогда при стыковании решений на соседних интервалах необходимо учитывать условия скачков.
Решение (8) относительно управляемой координаты Х при различных вещественных корнях характеристического уравнения имеет вид
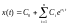(9)
где
-
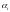корни характеристического уравнения,
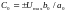(частное
решение уравнения 8), а постоянные
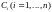зависят от начальных условий.
Пусть
на первом интервале управления
.
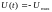Тогда, так как при переходе от одного
интервала управления к другому изменяется
знак управляющего воздействия, изменение
координаты Х во времени на отдельных
интервалах управления определяется
выражениями
(10)
где в последнем выражении будет знак "+", если - четно, и знак "-", если - нечётно.
Состыкуем
решения в моменты nepeключения
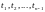для чего приравняем значения координаты
Х, получаемые из решения (10) на двух
соседних интервалах. Добавим также
условия в начальной и конечной точках.
В результате получаем
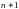уравнений:
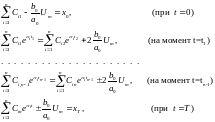(11)
Описанную
процедуру надо повторить для производных
,
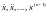принятых в рассматриваемом случае в
качестве фазовых координат системы.
Неизвестными в этой системе уравнений
являются
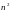постоянные интегрирования
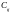
и
моментов переключения (включая момент
окончания процесса Т). Исключив из
системы уравнений постоянные
, получим систему из
алгебраических трансцендентных уравнений
относительно моментов времени
.
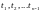Таким образом, задача отыскания
оптимального управления и оптимальной
траектории для линейного объекта сведена
к решению нелинейной алгебраической
системы из
уравнений. Эта система уравнений может
быть решена аналитически только для
простейших объектов управления. В общем
случае она решается численными методами,
такими как метод перебора всех возможных
значений корней с некоторым шагом, метод
последовательных приближений с выбором
шага по методу градиента или Ньютона.