
- •Основные понятия вариационного исчисления: функционал, непрерывный функционал, линейный функционал, вариация функционала.
- •Основные понятия вариационного исчисления: функционал, сильный и слабый экстремум функционала, условия экстремума.
- •Формировка простейшей вариационной задачи классического вариационного исчисления. Вывод уравнение Эйлера. Вывод уравнение Эйлера. Основная лемма вариационного исчисления.
- •Функционалы, зависящие от высших производных: уравнение Эйлера - Пуассона, условие Лежандра.
- •Задачи на условный экстремум: метод множителей Лагранжа.
- •Вариационные изопериметрические задачи. Особенности их решения.
- •Функционалы, зависимые от многих функций: уравнения Эйлера, условие Лежандра.
- •Определение функции Гамильтона, вспомогательные переменные, их смысл.
- •Понятия игольчатой вариации управления, принцип максимума л. С. Понтрягина.
- •Применение принципа максимума к объектам с линейным вхождением сигнала управления, двухточечная краевая задача.
- •Вид управления оптимального по быстродействию, теорема об n-интервалах.
- •Структура управления оптимального по быстродействию, определение моментов переключения.
- •Структура управления оптимального по быстродействию, определение знака управления на первом интервале.
- •7. Принцип оптимальности, понятие функции Беллмана.
- •8. Функция Беллмана, вывод функционального уравнения Беллмана.
- •9. Функциональное уравнение Беллмана, техника определения оптимального управления в методе динамического программирования.
- •10. Техника определения оптимального управления в методе динамического программирования, достоинства и недостатки динамического программирования.
- •Вопросы по теории акор
- •1. Постановка задачи управления Летовым а. М., ее решение методом динамического программирования.
- •2. Постановка задачи акор для линейных многомерных объектов, вывод уравнения Риккати.
- •3. Постановка нелинейной задачи акор, метод степенных рядов в ее решении.
- •4. Критерий обобщенной работы, основная теорема Красовского а. А.
- •5. Основная теорема Красовского а. А., особенности применения метода синтеза систем управления по критерию обобщенной работы к линейным объектам.
- •6. Основные понятия адаптивного управления. Адаптивная система со стабилизацией частотной характеристики разомкнутого объекта.
Применение принципа максимума к объектам с линейным вхождением сигнала управления, двухточечная краевая задача.
Многие реальные объекты управления с известным приближением могут быть описаны системой линейных дифференциальных уравнений. В связи с этим рассмотрим возможности принципа максимума при решении задачи оптимального быстродействия в линейных системах.
Пусть
объект управления n-го порядка с m
управляющими воздействиями описывается
уравнениями  (1)
(1)
где
 ,
,
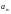 -
постоянные коэффициенты, а управляющие
воздействия ограничены по величине:
-
постоянные коэффициенты, а управляющие
воздействия ограничены по величине:
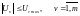 (2)
(2)
Составим функцию Гамильтона
 (3)
(3)
Согласно
принципу максимума оптимальное уравнение
должно обеспечить максимум функции
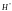 .
Анализируя (3), легко убедиться в том,
что функция
достигает максимума, если управление
выбрать в виде кусочно-постоянной
функции.
.
Анализируя (3), легко убедиться в том,
что функция
достигает максимума, если управление
выбрать в виде кусочно-постоянной
функции.
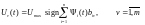 (4)
(4)
При
этом каждая составляющая вектора
управления должна изменяться в пределах
области управления
 независимо от остальных составляющих
и должна поддерживаться равной своим
предельным значениям.
независимо от остальных составляющих
и должна поддерживаться равной своим
предельным значениям.
При
 областью
допустимых управлений является интервал
областью
допустимых управлений является интервал
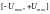 (рис.)
(рис.)
![]()
В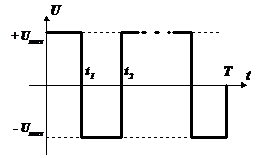 этом случае управление, доставляющие
максимум функции
,
имеет вид
этом случае управление, доставляющие
максимум функции
,
имеет вид
 (5)
(5)
Управление
удерживается на границе области
допустимых значений в каждый момент
времени
 за
исключением моментов
за
исключением моментов
 ,
когда
,
когда
 (рис.)
(рис.)
В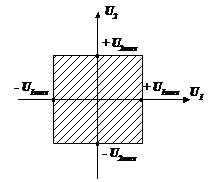 точках
точках
 значение
значение
 не определено. На интервале времени
не определено. На интервале времени
 оптимальное управление находится на
одном из своих предельных значений
оптимальное управление находится на
одном из своих предельных значений
 и изменяет знак при
и изменяет знак при
 после прохождения функции
после прохождения функции
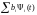 через нуль. Таким образом, оптимальное
по быстродействию управление является
релейным.
через нуль. Таким образом, оптимальное
по быстродействию управление является
релейным.
При
 ,
как видно из (4) вектор управления
,
как видно из (4) вектор управления
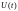 в процессе оптимального управления
принимает в пространстве управления
положения, соответствующие вершинам m
-мерного параллелепипеда допустимых
управлений. Например, при
в процессе оптимального управления
принимает в пространстве управления
положения, соответствующие вершинам m
-мерного параллелепипеда допустимых
управлений. Например, при
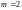 ,
управления принимают значения в вершинах
параллелограмма (рис).
,
управления принимают значения в вершинах
параллелограмма (рис).
В этом случае для произвольного момента времени существуют только четыре возможные комбинации управления (см. рис. 4)
 ,
,
 ,
,
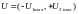 ,
,
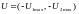
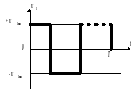

Рис. 4
Моменты
времени
 ,
в которые производится смена знака
управляющих воздействий, называются
моментами переключения. Эти моменты
переключения представляют собой корни
системы уравнений
,
в которые производится смена знака
управляющих воздействий, называются
моментами переключения. Эти моменты
переключения представляют собой корни
системы уравнений 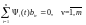 (6)
(6)
которые
могут быть найдены, если известны функции

 .
.
Функции являются решениями сопряженной системы дифференциальных уравнений, имеющей в рассматриваемом случае следующий вид:

 (7)
(7)
Однако
они не могут быть найдены непосредственно
путем решения системы уравнений (7),
поскольку неизвестны начальные условия
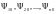 . Последние должны быть определены при
совместном решении сопряженной системы
уравнений и уравнений системы объекта
управления из условия, что оптимальная
траектория проходит через конечную
точку. Подставив выражение (4) для
. Последние должны быть определены при
совместном решении сопряженной системы
уравнений и уравнений системы объекта
управления из условия, что оптимальная
траектория проходит через конечную
точку. Подставив выражение (4) для
 в (1), получим вместе с (7) систему
в (1), получим вместе с (7) систему
 уравнений с
неизвестными и краевыми условиями:
уравнений с
неизвестными и краевыми условиями:
 (8)
(8)
 ;
;  (9)
(9)
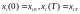 ;
; 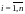 (10)
(10)
Таким
образом, при помощи принципа максимума
задача определения оптимального по
быстродействию уравнения
и оптимальной фазовой траектории
 сводится к двухточечной краевой задаче
для системы дифференциальных уравнений
(8)-(9). На пути решения краевых задач для
дифференциальных уравнений имеются
большие трудности, поскольку нет
аналитических способов определения
сводится к двухточечной краевой задаче
для системы дифференциальных уравнений
(8)-(9). На пути решения краевых задач для
дифференциальных уравнений имеются
большие трудности, поскольку нет
аналитических способов определения
 в явном виде и для их нахождения использует
приближенный метод (метод итераций).
Поэтому, при решении конкретных задач
оптимального по быстродействию управления
принцип максимума используется, как
правило, для определения формы оптимального
управления, а для нахождения параметров
управляющих воздействий, к которым
относятся моменты переключения и знак
на первом интервале, используют исходные
уравнения объекта и физические
соображения.
в явном виде и для их нахождения использует
приближенный метод (метод итераций).
Поэтому, при решении конкретных задач
оптимального по быстродействию управления
принцип максимума используется, как
правило, для определения формы оптимального
управления, а для нахождения параметров
управляющих воздействий, к которым
относятся моменты переключения и знак
на первом интервале, используют исходные
уравнения объекта и физические
соображения.
