1. Определение функции Гамильтона, вспомогательные переменные, их смысл.

Гамильтониан (функция Гамильтона) выглядит следующим образом:

(1)

(0=-1) и сравним ее с функцией Лагранжа (2):

(2)

Выразим вспомогательную функцию L через гамильтониан H:

(3)

(т.е. к функции H добавлено слагаемое, которое отличает ее от функции L).

Запишем необходимое условие экстремума (уравнения Эйлера-Лагранжа) с использованием функции H. Для частных производных, которые входят в уравнения Эйлера-Лагранжа (4) согласно (3) имеем (5)

(4) (5)

Подставим найденные выражения в (4), получим уравнения Эйлера-Лагранжа в канонической форме:

Рассмотрим физический (геометрический) смысл уравнений (6).

Уравнения (6.1) являются уравнениями объекта. Уравнения (6.2), записанные относительно вспомогательных переменных , образуют так называемую сопряженную к (6.1) систему. Они имеют вид:

Уравнения (6.3) являются алгебраическими, а не дифференциальными. Значения функции, удовлетворяющие условию в виде (6.3), называются стационарными значениями функции, а точки пространства аргументов, в которых эти условия выполняются - стационарными точками (стационарными называются точки, в которых производная функции равна нулю). Следовательно, оптимальное управление есть стационарная точка функции Гамильтона.

Гамильтон для механической системы имеет следующий физический смысл: это полная энергия механической системы.

2. Понятия игольчатой вариации управления, принцип максимума л. С. Понтрягина.

Пусть объект управления описывается уравнением: . (1)

Управления при каждом принимают значения из некоторого замкнутого множества. В качестве такого множества можно, в частности, иметь в виду множества:

, . (2)

Назовем допустимыми управления те , которые являются кусочно-непрерывными функциями ( ) и принимают значение из множества .

Задача управления формулируется следующим образом. Среди допустимых управлений, переходящих объект (1) из заданного состояния: (3) в другое заданное состояние (4), требуется найти такое, для которого функционал (5) принимает наименьшее значение.

Подчеркнем, что в отличие от общей задачи Лангранжа, приведенной ранее, здесь имеются следующие особенности: 1) присутствуют ограничения вида (2); 2) функции управления принадлежат классу , а не классу гладких функций .

3) кроме того, в (1) и (5) функции , , не зависят явно от .

Последнее условие (стационарность объекта) не снижает общность рассмотрения, так как в противном случае, вводя новую переменную и дополняя систему (1) уравнением , получим объект, правая часть которого не зависит явно от .

Если в процессе оптимального управления функции , не достигают границ множества (2), то нахождения этих уравнений можно использовать канонические уравнения Эйлера:

, (6) , (7) , . (8)

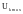Однако часто оптимальное управление принимает граничные значения , либо 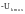, , более того, оптимальное управление может скачком переходить с одной границы на другую. Такие управления уже являются кусочно-непрерывными функциями времени.

В случае попадания оптимального управления на границу множества оптимальные управления удовлетворяют принципу максимума Л.С. Понтрягина, установленного и доказанного в форме следующей теоремы.

Теорема. Пусть , , решение задачи (1)(5). Тогда существует непрерывная вектор-функция и постоянная , такие, что:

1) является решением сопряженной системы (7), соответствующей рассмотренному решению , ;

2) при каждом функция Гамильтона H(0, ,X,U) переменного достигает в точке максимума:H(0, ,X,U) =max H(0, ,X,U ) . (9)

3) если (t), , , удовлетворяют (6), (7), (9), то функции и переменного являются постоянными и равными нулю.

Таким образом, согласно приведенной теореме управление , переводящее объект из заданного начального состояния в заданное конечное , только в том случае окажется оптимальным, если найдутся постоянная и отличное от нуля решение системы (7), при которых вдоль рассматриваемой траектории функция все время будет достигать наибольшего, постоянного во времени, значения по переменной : .

Центральное место в этой теореме занимает условие максимума функции , вследствии чего необходимое условие оптимальности, сформулированное теоремой, называется принципом максимума.

Принцип максимума устанавливает необходимые условия сильного экстремума функционала, т.е. экстремума в классе кусочно-непрерывных функций . Это следует из того, что в принципе максимума варьирование управлений осуществляется на бесконечно малом интервале , и вариация представляет импульс бесконечно малой длительности , амплитуда которошо может быть любой, но не должно выводить управление за область существующих ограничений. Подобная вариация называется игольчатой. Таким образом проварьированное управление является кусочно-непрерывным с разрывами первого рода, что обеспечивает установление условий сильного экстремума функционала (5).

Рис. 1. Игольчатая вариация управления