Функционалы, зависимые от многих функций: уравнения Эйлера, условие Лежандра.

Одним из обобщений простейшей вариационной задачи является задача отыскания экстремума функционала, зависящего от n функций (1) при заданных граничных значениях для всех функций (2)

Требуется в классе функций C₁[t₀,t₁] найти функции x_i(t), i=1,2,…,n, проходящие через граничные точки (2) и доставляющие минимум функционалу (1).

Для получения необходимых условий экстремума рассматриваемого функционала будем варьировать лишь одну из функций x_i(t), i=1,2,…n, оставляя все остальные функции неизменными. При этом функционал превращается в функционал, зависящий лишь от одной варьируемой функции, например, от x_j(t) = и следовательно, функция, реализующая экстремум, должна удовлетворять уравнению Эйлера

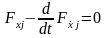. Так как это рассуждение применимо к любой функции x_j, j=1,2…,n ,то получаем систему дифференциальных уравнений Эйлера 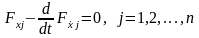, (3) которая определяет совокупность необходимых условий экстремума вариационной задачи (1), (2).

Экстремали, соответствующие системе (3), содержат 2n постоянных интегрирования, находящихся из заданных граничных условий (2).

Полученный результат часто записывают в матричной форме. Введем в рассмотрение вектор и запишем функционалл (1) в следующем виде

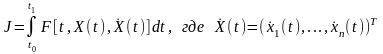
Используя понятие производной скалярной функции 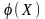от векторного аргумента Х

,условия (3) можно записать в компактной матричной форме 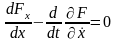. (4) (полный аналог скалярного уравнения Эйлера).

Используя матричные операции легко записать условия Лежандра для функционала (1). С этой целью введем в рассмотрение матрицу (Матрица Гессе, производные по индексам) которая является аналогом скалярного выражения .

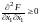
Для достижения на некоторой совокупности экстремалей минимума функционала (1) необходимо, чтобы все угловые миноры этой матрицы были неотрицательны, т.е. 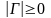, В математике условия (6) известны как необходимые и достаточные условия Сильвестра положительной определенности матрицы Г. Для достижения максимума J неравенства (6) должны иметь противоположный знак. Функционал (1) может содержать производные высших порядков. В этом случае система уравнений будет состоять из уравнений Эйлера-Пуассона.

Применение классического вариационного исчисления к задаче оптимального управления, двухточечная краевая задача.

Применение классического вариационного исчисления к задаче оптимального управления, уравнения Эйлера - Лагранжа в канонической форме.

Вспомним теперь формулировку задачи оптимального управления с закрепленными концами. Объект управления описывается уравнениями .

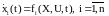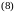
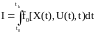
Требуется найти вектор управляющих воздействий u(t) и соответствующую фазовую траекторию x(t) при условии, что X(t₀) = X₀, X(t_k) = X_k и функционал принимает экстремальное значение.

Очевидно, что сформулированная задача по существу является вариационной задачей и отличается от обычной вариационной задачи на условный экстремум только тем, что в нее входят два вида функций: функция X(t), характеризующая состояние системы, и функция управления U(t).Это отличие не принципиально и легко показать, что задача оптимального управления, удовлетворяющая основным положениям классического вариационного исчисления (отсутствие ограничений на фазовые координаты и управляющие воздействия, непрерывность и дифференцируемость управляющих воздействий), является общей задачей Лагранжа. Действительно, интеграл (9) можно рассматривать как функционал, зависящий от n+m функций x₁,…,x_n, u₁,…,u_n.

Эти функции связаны дифференциальными уравнениями объекта (8), которые можно записать в виде уравнений связи

. (10)

Следовательно, для решения задачи оптимального управления, которая удовлетворяет основным положениям классического вариационного исчисления, можно использовать метод неопределенных множителей Лагранжа и записать необходимое условие экстремума функционала (9) при наличии ограничения (10) в виде уравнения Эйлера – Лагранжа. Согласно методу неопределенных множителей введем вспомогательный функционал

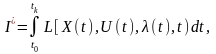(11) где 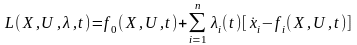(12)

есть функция Лагранжа. Тогда уравнение Эйлера-Лагранжа будут иметь вид

(13)

В дальнейшем будем использовать, так называемую каноническую форму записи уравнений Эйлера-Лагранжа. Такая форма записи уравнения Эйлера-Лагранжа имеется в вариационном исчислении мы рассмотрим ее применительно к задачам оптимального управления.

Введем функцию, называемую гамильтонианом (функция Гамильтона).

(14)

(₀=-1) и сравним ее с функцией Лагранжа (12). Выразим вспомогательную функцию L через гамильтониан H:

(15)

(т.е. к функции H добавлено слагаемое, которое отличает ее от функции L).

Запишем необходимое условие экстремума (уравнения Эйлера-Лагранжа) с использованием функции H. Для частных производных, которые входят в уравнения Эйлера-Лагранжа (13) согласно (15) имеем (16) подставим найденные выражения в (13), получим уравнения Эйлера-Лагранжа в канонической форме :

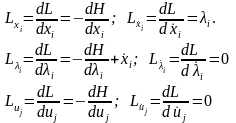(16)

Здесь уравнения (17а) являются уравнениями объекта (8). Уравнения (17б), записанные относительно вспомогательных переменных , образуют так называемую сопряженную к (17а) систему. Они согласно (14) имеют вид :

Уравнения (17в) являются алгебраическими. Действительно

Заметим, что значения функции, удовлетворяющие условию в виде (17в), называются стационарными значениями функции, а точки пространства аргументов, в которых эти условия выполняются - стационарными точками (стационарными называются точки, в которых производная функции равна нулю). Следовательно, оптимальное управление есть стационарная точка функции Гамильтона.

Уравнения (19) позволяют определить управление в виде функции . (20)

П одставив (20) в (17а и б), получим систему дифференциальных уравнений:

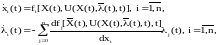(21) X(t₀)=X₀ , X(t_k)=X_k .

Общее решение такой системы, как известно, зависит от 2n параметров (начальных условий) поскольку управление найдено как функция (X и ). В задаче с закрепленными концами n параметров задано на левом конце фазовой траектории (X(t₀)=X₀), и n параметров на правом конце (X(t_k)=X_k). Такая задача называется краевой.

Таким образом решение задачи оптимального управления оказалось сведенным к решению краевой задачи для систем дифференциальных уравнений. Уравнений Эйлера-Лагранжа решения системы (17) не обязательно дают оптимальное управление, но только такие решения могут претендовать на роль оптимального управления. С помощью уравнений Э-Л обычно удается найти оптимальное управление и оптимальную траекторию системы, поскольку существование и характер экстремума функционала в конкретной задаче оптимального управления, как правило, известно заранее.

ОТВЕТЫ ПО НЕКЛАССИЧЕСКОМУ ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ