Задачи на условный экстремум: метод множителей Лагранжа.

Решение многих технических вопросов приводит к таким вариационным задачам, в которых функции, доставляющие экстремум должны, кроме того, удовлетворять некоторым дополнительным условиям. Так, например, в задаче о кратчайшей морской трассе на поверхности земного шара нужно найти минимум функционала – длины кривой

(1)

при условии, что эта кривая лежит на поверхности земного шара, т.е. удовлетворяет уравнению сферы 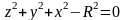. (2)

Экстремум функционала, определяемый при таком дополнительном условии называется условным экстремумом.

Наиболее простой в методическом плане способ решения указанной задачи на условный экстремум состоит в следующем. Из уравнения (2) выражаем функцию z(x) через функцию y(x)

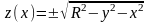
и дифференцируем ее по х:

. (3)

Подставляем функцию (3) в функционал (1)

. (4)

Таким образом исходная задача на условный экстремум (1), (2) сведена к стандартной задаче на поиск экстремума функционала (4).

Однако необходимо подчеркнуть, что указанная процедура исключения неизвестных приводит часто к сложным вычислениям, а во многих случаях не может быть выполнена точно аналитически. В связи с этим Лагранжем был предложен другой достаточно простой метод решения – метод неопределенных множителей (множителей Лагранжа).

Сформулируем в общем виде задачу на условный экстремум.

Пусть задан функционал

(4)

при наличии условий i=1,…,m, m<n (5)

и

X(t₀) = X₀; X(t_k) = X_k; X = (x₁,x₂,…,x_n)^T . (6)

Функции i=1,…,m предполагаются гладкими и независимыми по переменным x₁,…,x_n .

Теорема. Если X(t) – экстремаль функционала (4), удовлетворяющая условиям (5),(6), то она удовлетворяет уравнениям Эйлера, составленным для функционала

, (7)

где - соответствующим образом подобранные функции (множители Лагранжа).

В соответствии с данной теоремой, экстремали функционала (4) и функции , i=1,…,m должны удовлетворять уравнениям:

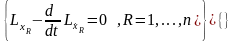, (8)

где

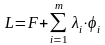(9)

так называемая функция Лагранжа.

Таким образом экстремаль задачи (4) - (6) определяется обычными методами поисками экстремалей функционала

.

Вариационные изопериметрические задачи. Особенности их решения.

Как частный случай задачи Лагранжа можно рассматривать и представляющую самостоятельный интерес изопериметрическую задачу, когда условия, которым подчинена искомая функция, заданы в интегральной форме. Например, простейшая задача формулируется следующим образом: определить экстремум функционала

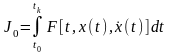(1)

при условии, что другой функционал

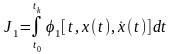(2)

сохраняет заданное значение С, а экстремаль проходит через точки: x(t₀)=x₀; x(t_k)=x_k. Название изопериметрических такого рода задачи получили по названию одной из них: среди всех кривых равной длины (одинакового периметра) найти ту, которая ограничивает наибольшую площадь. Эта задача была известна еще древним грекам под названием «задача Дидоны». По преданию, легендарная основательница Карфагена царица Дидона покупала у туземцев землю, на которой должен быть основан город. Ей согласились продать лишь участок, который можно охватить бычьей шкурой. Тогда Дидона разрезала шкуру на тонкие ремни и расположила их так, чтобы охватить наибольшую площадь. Если пользоваться современными математическими понятиями, Дидона решила именно изопериметрическую задачу, выбирая функцию y(x), доставляющую максимум интегралу

(3)

(площади, охваченной ремнем), при заданном значении интеграла

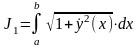(4)

(длина ремня).

Изопериметрическую задачу легко свести к общей задаче Лагранжа. Действительно, обозначив

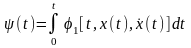(5)

(интеграл с переменным верхним пределом), получим

(6)

и приходим к следующей задаче Лагранжа: найти функции x(t), , доставляющие экстремум функционалу (1) при наличии уравнения связи .

Согласно теореме, для решения этой задачи следует составить уравнение Эйлера для вспомогательной функции (7) которые будут иметь вид

. (8)

Из второго уравнения (8) следует, что 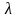=const, т.е. для изопериметрической задачи множитель Лагранжа обращается в постоянное число. В тоже время это уравнение не дает никакой информации о функции , однако в этом и нет необходимости: ведь мы должны найти только одну функцию x(t), доставляющую экстремум функционалу (1) при наличии условия (2). Для этого достаточно одного уравнения – первого уравнения системы (8), в котором .

Таким образом, получаем следующее мнемоническое правило: для того чтобы найти функцию x(t), доставляющую экстремум интегралу (1) при условии, что интеграл (2) сохраняет заданное значение, следует составить одно уравнение Эйлера для промежуточной функции

. (9)

В решение уравнения Эйлера будут входить три произвольные постоянные – две постоянные интегрирования и постоянная 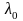. Для их определения имеем как раз три уравнения: два уравнения следуют из условий прохождения экстремали через две заданные точки, а третье – из условия, что интеграл (2) равен заданному значению С.

Применяя это правило к задаче Дидоны можно установить, что ее решение является окружностью с радиусом . Так при этом значение функционала равно С, то отсюда находим значение множителя Лагранжа .