Функционалы, зависящие от высших производных: уравнение Эйлера - Пуассона, условие Лежандра.

Экстремали функционала (1) закрепленными концами (2) удовлетворяют условию Эйлера (10), которое выражает первое необходимое условие экстремума. Однако осталось неясным, доставляют ли они функционалу (1) максимум или минимум? Ответ на этот вопрос дает теорема Лежандра, выражающая второе необходимое условие экстремума: для того чтобы функционал (1) в задаче с закрепленными границами на кривой x(t) достигал минимума (максимума), необходимо, чтобы вдоль этой кривой выполнялось условие

- минимум ( - максимум) .

Эту теорему примем без доказательства, но укажем, что приведенное условие непосредственно получается после раскрытия второй вариации функционала ²V, так как для того чтобы функция x(t) доставляла минимум функционалу V[x(t)], необходимо, чтобы ²V0 (здесь наблюдается полная аналогия с задачей на минимум функции f(t), для которой условие минимума записывается так: 1) df=0; 2) d²f0.).

Если производная 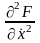тождественно равна нулю, что возможно в случаях, когда функция F[…] не зависит от 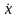или зависит линейно, то вторая производная экстремали 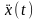не существует. Такие функционалы называют вырожденными, они имеют особые свойства.

Уравнение Эйлера – Пуассона

Простейшую вариационную задачу можно обобщить на случай, когда подынтегральная функция содержит производные высших порядков и функционал имеет вид

. (1)

Здесь функция F предлагает (n+2) раза дифференцируемой по всем аргументам, а граничные условия заданы в форме

(2)

т.е. в граничных точках заданы значения не только функции, но и ее производных до порядка (n-1) включительно (всего 2n условий).

Решение задачи J = min ищется в классе C_2n[t₀,t₁] гладких 2n раз дифференцируемых функций. Методика получения необходимого условия минимума функционала остается прежней: находится первая вариация критерия и приравнивается к нулю, что после преобразований приводит к уравнению

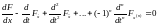, (3)

которые называются уравнением Эйлера-Пуассона и представляет в общем случае нелинейное дифференциальное уравнение 2n-порядка.

Его решение x(t,c₁,c₂,…,c_2n) содержит 2n постоянных интегрирования. Последние находятся на основании такого же количества граничных условий (2).

Дадим вывод уравнения (3), ограничившись для простоты выкладок случаем, когда функционал зависит от производной не старше второго порядка:

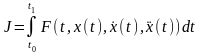. (4)

Предположим, что экстремум достигается на функции x(t), и прибавим к ней вариацию 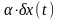такую, что на концах при t=t₀ и t=t₁ как 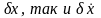обращаются в нуль.

Определим вариацию функционала

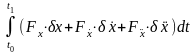. (5)

Преобразуем теперь выражение (5), пользуясь формулой интегрирования по частям, причем третий член вариации будем интегрировать по частям дважды:

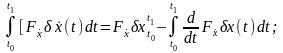(6)

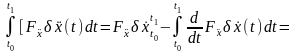
. (7)

Вследствие условий на концах участка все неинтегральные члены обращаются в нуль, и, следовательно, на основе (5) - (7) получаем

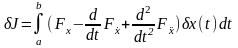. (8)

Поскольку необходимым условием экстремума является равенство нулю первой вариации функционала, а вариация произвольна, то из равенства и леммы Лагранжа (основной леммы вариационного исчисления) следует уравнение (3).

В этом случае имеет место следующий аналог условия Лагранжа, позволяющий отличить максимум от минимума функционала (1): если функция x(t) доставляет минимум (максимум) функционалу, необходимо, чтобы ).
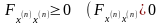