6. Основные понятия адаптивного управления. Адаптивная система со стабилизацией частотной характеристики разомкнутого объекта.

Общие понятия об адаптивном управлении. Для математической формулировки и последующего решения задачи синтеза оптимальной системы уравнения необходимо располагать определенными сведениями об объекте управления в условиях работы системы. Объект управления должен быть ма­тематически описан, т.е. найдено его дифференциальное уравнение или какой-нибудь аналог уравнения. Также должно быть детерминированном или вероятном смысле известны свойства задающих и возмущающих воздействий. Наличие такой априорной информации позволяет синтезировать оптимальную и неоптимальную систему, но имеющую нужные показатели качества. Во многих реальных ситуациях информация о свойствах объекта управления и внешних воздействиях оказывается недостаточной для построения системы с необходимыми показателями качества.

Эта недостаточность может носить двоякий характер. В первом случае на этапе проектирования структуры и расчета параметров. УУ или некоторой его части могут оказаться полностью или частично не известными свойствами ОУ и внешних воздействий. Сис­тема управления в процессе функционирования сама должна автоматически восполнять недостающую информацию и по мере ее поступления изменять структуру и параметры УУ так, чтобы показатель качества или достигал экстремального значения, или соответствовал заданным огра­ничениям. После восстановления всей недостающей информацией при У неизменных в последующем свойствах ОУ и внешних воздействиях процесс изменения структуры и параметров УУ прекращается и система работает в обычном режиме.

Во втором случае имеются исходные сведения о свойствах ОУ и внешних воздействий, позволяющих синтезировать УУ. Однако в процессе работы системы эти свойства в силу различных причин мо­гут изменяться, поэтому заранее достоверно прогнозировать характер изменения не удается. Эти изменения, если они происходят в доста­точно большом диапазоне, могут привести к тому, что УУ, спроектированное в ориентации на некоторую начальную информацию, в новых условиях уже не обеспечит соответствие показателя качества существующим ограничениям. Качество может оказаться не экстремальным, т.е. в новых условиях система не будет оптимальной, или выйдет из требуемого диапазона.

Две перечисленные ситуации изменения свойств ОУ и внешних воздействий не исключают возможнос­ти существования третьей, в которой необходимая для синтеза УУ информация может быть как неизвестна на начальном этапе так и подвер­гаться непрогнозируемым изменениям в последующем. Однако незави­симо от конкретизации ситуации общим для всех отмеченных случаев является то, что система управления в процессе функционирования должна реагировать на изменение свойств ОУ и внешних воздействий и на основании результатов обработки соответствующей информации приспосабливаться к новым условиям путем изменения структуры и параметров УУ или некоторой его части так, чтобы показатель ка­чества каждый раз достигал экстремального значения или находился в заданном диапазоне. Такие системы автоматического управления принято называть адаптивными, а процесс изменения структуры и па­раметров УУ, осуществляемый на основании информации о свойствах ОУ и внешних воздействий и обеспечивающий приспосабливаемость системы к изменяющимся условиям работы, адаптацией. Если адаптация обусловлена только отсутствием начальной ин­формации о свойствах ОУ и внешних воздействий и после ее воспол­нении из-за неизменности этих свойств необходимое качество управления обеспечивается при неизменных структуре и параметрах УУ, адаптацию принято называть однократное. В остальных случаях коррекция управляющего устройства осуществляется каждый раз при изменении свойств ОУ или внешних воздействий и адаптация называ­ется многократной.

СНС со стабилизацией амплитудно-частотных характеристик. При построении систем управления очень важно иметь возмож­ность поддерживать свойства замкнутой системы неизменными в ши­роком диапазоне изменения свойств ОУ. Свойства линейной замкнутой системы удобно оценивать по виду ее амплитудно-частотных характеристик или импульсной характеристики. Соответствующие системы, если эффект стабилизации обеспечивается рациональным из­менением параметров УУ на основании получаемой в процессе рабо­ты системы информации об ОУ принято относить к СНС со стабилиза­цией качества управления. Характерным для таких систем является наличие модели, отражающей желаемые свойства замкнутой или разомкнутой системы.

Пусть проектируется система управления минимально фазовым ОУ, особенность которых состоит в возможности исследования их частотных свойств только по виду АЧХ.

Предусмотрим в структуре УУ корректирующие цепи с переменными параметрами, изменяющимися в процессе работы системы при изменении свойств ОУ. Число m таких параметров целесообразно выбрать рав­ным числу переменных параметров в уравнении ОУ, хотя из соображе­ний простоты технической реализуемости число m может быть умень­шено. Параметры корректирующих цепей следует изменять так, чтобы свойства проектируемой системы были тождественны свойствам модели при всех состояний ОУ. Для этого можно на m частотах измерить АЧХ разомкнутой системы и полученные результаты сравнить с аналогичными значениями модели. На основании результатов сопоставления изменяются параметры УУ в направлении устранения рассогласования. Схема реализации такого исхода изображена на рис. 1.

Основной контур включает в себя объект управления, характе­ризующийся медленно изменяющимися в системе параметрами. Эта "мед­ленность" позволяет СУ вместе с неизменной частью УУ на интервалах времени, соизмеримых с длительностью переходных процессов, харак­теризовать передаточной функцией W0(p). В основной контур вхо­дит и корректирующее устройство, состоящее из m параллельно соединенных цепей с переменными коэффициентами ai (положит, сигналы с выходов интеграторов, подаваемые на умножители) и фильтрами Wi(p), 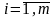. Выбор функций Wi(p) и диапазон изменения коэффициентов ai должны быть подчинены следующему достигаемому во всей области изменения параметров ОУ условию: (1) в котором левая часть представляет собой передаточную функций разомкнутой проектируемой системы. [WM(p)] - передаточная функ­ция модели. Условие (1) считается приближенно достигнутым, если выпол. равенство (2) т.е. у проектируемой системы АЧХ совпадает с АЧХ модели на m частотах . Последние должны равномерно покрывать всю полосу пропускания модели. Чтобы (2) заведомо имели действи­тельные решения относительно ai, в качестве фильтров Wi(p) выбирают узкополосные устройства, обладающие свойствами при , тогда из (2)следует (3)

Для выбора только положительных величин коэффициентов, что обеспечивает, однозначность решения (3) схемой предусмотрена система детекторов Д, которые пропускают лишь положительные входные сигналы и образуют на выходах нули при отрицательных входных сигналах. На вход системы для контроля за частотными свойствами помимо основного подается пробный сигнал 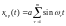, содержащий весь спектр частот .

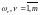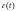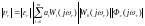Сигнал рассогласования подается на вход модели. Сиг­налы с выходов модели и системы преобразуются m узкополосными резонансными фильтрами с передаточными функциями , , настроенными на рабочие частоты , т.е. из всего спектра входных сигналов - пропускающими частоты» близкие к . Сигналы с выходов фильтров выпрямляются детекторами, так что для установившегося режима можем записать , (4) , (5) где амплитуда - гармоники спектра сигнала .

Сигналы (4) и (5) попарно вычитаются и подаются на входы ин­тегралов с пер. функ. 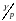. Положительные сигналы с выходов интеграторов пропускаются детекторами представляют собой значения коэффициентов настройки корректирующих цепей, которые при условии 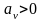подчинены уравнениям. 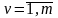. Последнее уравнение можно переписать в диф. форме ; , что с учетом (4) и (5) можно представить в виде

(6) где , .

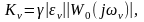Соотношения (6)являются уравнениями контура самонастройки и показывают, что при изменении свойств ОУ величины 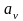должны меняться до тех пор, пока не бу­дут выполнены условия совпадения (2) АЧХ проектируемой системы и модели. Если выполняется условие 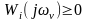при уравнения (6) становятся независимыми, так что , (7) Этим уравнением первого порядка соответствуют всегда устой­чивые процессы, поэтому при любых начальных значениях коэффициен­тов в последующем установятся такие значения, при которых бу­дет достигнут результат самонастройки (2), т.е. независимо от изменения свойств ОУ свойства всей системы будут соответствовать модели.

52