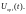3. Постановка нелинейной задачи акор, метод степенных рядов в ее решении.

Постановка нелинейной задачи АКОР. Рассмотрим объект управления, описываемый уравнениями: 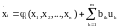, 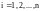. (1)

В фазовом пространстве, определяемом вектором , данный объект описывается матричным уравнением: , (2)

где ; ; .

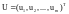Предположим, что правые части этих уравнений разложимы в ряд Тейлора в окрестности точки , . Тогда уравнения (1) принимают вид:

, . (3)

Требуется найти уравнения , , (4)

при которых на движениях системы (3), (4), возбужденных произвольными начальными отклонениями 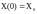, минимизируется квадратичный функционал:

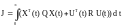. (5)

Решение этой задачи получено в работах Альбрехта Э.Г., Зубова В.И.

Решение нелинейной задачи АКОР для объекта первого порядка.

Для простоты демонстрации особенностей решения нелинейной задачи АКОР проанализируем данное решение при 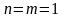, т.е. для объекта первого порядка:

. (6)

Для решения задачи применяем динамическое программирование: , (7)

где -производные функции Беллмана, 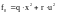- интегрант критерия (5) для объекта первого порядка.

Для определения оптимального управления записываем частную производную по 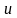от функции (7): .

Отсюда находим структуру оптимального управления: . (8)

Подставляя управление (8) в уравнение (7), приходим к необходимости решения следующего уравнения в частных производных – уравнения Гамильтона-Якоби-Беллмана:

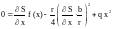. (9)

Решение этого уравнения будем искать в форме степенного ряда:

. (10)

Подставляя (10) в (9), получим:

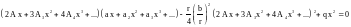. (11)

Приравнивая нулю совокупность коэффициентов при одинаковых степенях 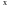, получим уравнения для определения неизвестных параметров 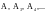функции Беллмана (10). Так, например, для совокупности коэффициентов при имеем: . (12)

Для совокупности коэффициентов при 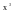получаем: . (13)

Приравнивая нулю совокупность коэффициентов при 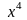, устанавливаем:

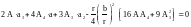. (14)

Уравнение (12) совпадает с уравнением (11) предыдущей лекции и его решение имеет вид: 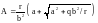. (15)

Уравнение (13) перепишем в виде: .

С учетом соотношений (13), (14) предыдущей лекции последнее уравнение представляем в форме: . (16)

Уравнение (16) в отличии от (12) является линейным, которое легко решить относительно искомого коэффициента: 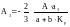. (17)

Подчеркнем, что это решение существует, если . Последнее условие выполняется в силу асимптотической устойчивости уравнения , описывающего замкнутую оптимальную систему с линейным объектом .

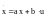В аналогичном виде можно представить уравнение (14):

, (18)

из которого однозначно определяется параметр .

Таким образом, в соответствии с (8) искомое управление имеет вид:

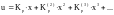, (19)

где ; ; 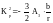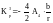. (20)

4. Критерий обобщенной работы, основная теорема Красовского а. А.

Основная теорема Красовского А.А.. Рассмотренные ранее трудности решения нелинейной задачи АКОР в постановке Летова-Калмана вызвали создание А.А. Красовским нового метода синтеза оптимальных систем – аналитического оптимальных регуляторов по так называемому критерию обобщенной работы. Сохраняя матричное описание объекта управления и критерия качества предыдущей лекции, критерий обобщенной работы можно записать так

. (1)

Этот критерий качества называется полуопределенным в связи с тем, что он отличается от квадратичного метода Летова–Калмана наличием дополнительного слагаемого

, (2)

зависящим от неизвестной функции Беллмана S(X).

В данном случае оптимальный закон управления определяется следующей теоремой.

Теорема: для процесса, описываемого управлением

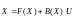(3)

в смысле минимума функционала (1) являются уравнения

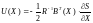, (4)

где S(X) – есть вынужденные решения уравнения в частных производных

(5)

Строгое (длинное) доказательство данной теоремы, приводимое в работах А.А. Красовского, повторять не будем. Однако отметим, что указанный результат можно получить, повторив рассуждение (18)-(28) предыдущей лекции, предварительно обозначив

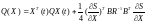. (6)

В этом случае вместо уравнения (28) получаем

.

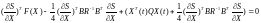После сокращения слагаемых уравнение принимает вид

, (5*)

эквивалентный уравнению (5). Это рассуждение не является математически строгим, так как здесь предполагается, что функция Q(X) является полностью известной (заданной), хотя она согласно (6) выражается через искомую функцию Беллмана. Но оно объясняет, подтверждает результат А.А. Красовского.

Последние выкладки показывают, что Красовский А.А. специально ввел в квадратичный функционал слагаемое (2), чтобы вместо сложного нелинейного уравнения (28) получить более простое линейное уравнение (5), решение которого определяет оптимальное уравнение (4). Уравнение (5) в литературе известно как уравнение Ляпунова А.М. Принципиальная особенность метода синтеза А.А. Красовского и состоит именно в решении уравнения Ляпунова (5) вместо решения уравнения Беллмана (28). Эта особенность метода имеет важные практические последствия: если для объектов высокого порядка вычислительные трудности решения нелинейного уравнения (28) трудно преодолимы, то и определение решений линейного уравнения (5) для тех же объектов не встречает больших затруднений. Данная главная особенность метода А.А. Красовского определяет и его последующие свойства.

Физический смысл критерия А.А. Красовского. Широкое распространение на практике метода А.А. Красовского определяется не только тем, что он существенно уменьшает объем вычислений в сравнении с методом Летова-Калмана, но и тем, что используемый функционал качества имеет глубокий физический смысл.

Для выяснения физического смысла критерия (1) рассмотрим частный его случай, когда матрица R является диагональной

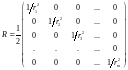. (7)

В этом случае в соответствии с (4) оптимальное управление определяется выражением

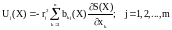. (8)

Соответственно критерий (1) запишется в виде

(9)

где оптимальные управления 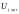описываются уравнениями (8).

Функционал (9) называется критерием обобщенной работы. Это название связано с тем, что последнее слагаемое в (9) можно записать как интеграл , который выражает собой энергию (обобщенную работу) оптимального управления