Вопросы по теории акор

1. Постановка задачи управления Летовым а. М., ее решение методом динамического программирования.

Постановка задачи управления по Летову А.М.

Пусть имеется стационарный объект управления, движение которого описывается векторно-матричным уравнением:

. (1)

Здесь составляющие xi, i = 1, 2, . . . n вектора X имеют смысл отклонений траектории от заданного (невозмущенного) движения; U – вектор m управляющих воздействий, требуется найти закон управления:

, (2)

который в совокупности с объектом (1) образует асимптотически устойчивую систему, переводящий ее из начального состояния X0 = X(t=0) в конечное нулевое состояние X(t→∞) = 0 с минимальным значением функционала:

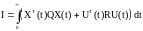, (3)

где Q, R − симметричные, вещественные, положительно-определенные матрицы размерностей nn и mm. Напомним, что матрица Q называется положительно-определенной, если квадратичная форма Q(X) = XTQX > 0 для всех X за исключением X=0. Далее это обозначается неравенством Q>0.

Подчеркнем, что на координаты векторов X, U ограничения не накладываются.

Решение задачи Летова для объекта первого порядка

В этом случае (n = m = 1) уравнение объекта и функционал принимает вид:

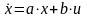, (4)

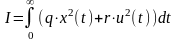. (5)

Для решения задачи применим метод динамического программирования, основное функциональное уравнения которого записывается так:

, (6)

где

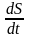= = (7)

− производная функции Беллмана, f0 = qx2 + ru2 − интегрант критерия (5).

Для нахождения оптимального управления записываем частную производную по u от функции в фигурных скобках:

.

Отсюда определяем структуру оптимального управления

. (8)

Подставляем управление (8) в уравнение (6), преобразованное с учетом (7):

. (9)

Таким образом, решение задачи АКОР свелось к решению нелинейного уравнения в частных производных (9).

Так как объект стационарный, то решение этого уравнения при краевом условии S[x(t1)] = 0, t1→∞ будем искать в виде квадратичной функции

, A = const. (10)

Подставляя это выражение в уравнение (9), получим

.

Отсюда с учетом, что x ≠ 0, следует алгебраическое уравнение для определения коэффициента А функции Беллмана

. (11)

Из двух решений

(12)

этого уравнения выбираем первое, исходя из условия положительности функции S(x), обеспечивающего асимптотическую устойчивость синтезируемой системы, а, следовательно, и выполнение краевого условия S[x(∞)] = 0.

На основе уравнения (8) определяем оптимальный закон управления

. (13)

Таким образом, оптимальным регулятором в задачах управления (4), (5) является пропорциональный (П) регулятор u = Kp∙x с коэффициентом усиления

. (14)

2. Постановка задачи акор для линейных многомерных объектов, вывод уравнения Риккати.

Применяя матричные операции, полученное в предыдущей шпоре решение можно распределить на решение многомерной задачи АКОР (1) - (3).

Напомним, что дифференцирование скалярной функции f(x) по векторному аргументу X определяется следующим образом:

.

Рассмотрим функцию f(X,Y) = YTBX, где B − матрица размерности nn. Для этой функции справедливо соотношение:

, (15)

. (16)

Это соотношение легко проверить для двумерных векторов

(17)

Для функции (17) находим

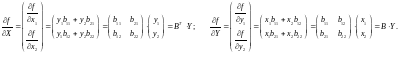
Таким образом, соотношения (15), (16) действительно имеют место.

Для решения задачи (1)(3) применяем также метод динамического программирования

. (18)

Учтем, что . (19)

Введем в рассмотрение вектор 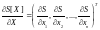, (20)

с помощью которого выражение (19) можно записать так

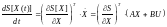. (21)

Подставляем (21) в (18): 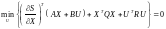. (22)

Для определения оптимального управления дифференцируем выражение в фигурных скобках по вектору U с учетом того, что

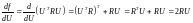, (23)

получаем

.

Отсюда находим оптимальное управление

, (24)

которое по форме полностью аналогично управлению (8) для объекта первого порядка.

Подставим это управление в (22):

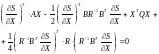(25)

Последнее слагаемое в (25) преобразуется к виду

(26)

с учетом симметрии матрицы R=RT и матричного равенства

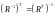. (27)

На основе (25), (26) записываем уравнение

. (28)

Решение уравнения в частных производных (28), которое является многомерным аналогом уравнения (9) – уравнения Гамильтона-Якоби-Беллмана, будем по аналогии определять в квадратичной форме 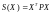, P=PT, P>0. (29)

Повторяя преобразование (23), можно получить . (30)

С использованием (30) уравнение (28) приводится к виду

.

С учетом симметрии матрицы R*=BR-1BT и X0, последнее уравнение преобразовывается к виду 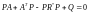. (31)

Таким образом, согласно (24), (29) оптимальное управление описывается выражением

, (32)

в котором матрица Р находится решением уравнения Риккати (31), т.е. оптимальное управление (32) представляет собой многомерный пропорцинальный П-регулятор с коэффициентами усиления .
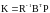