9. Функциональное уравнение Беллмана, техника определения оптимального управления в методе динамического программирования.

Функциональное уравнение Беллмана:

(8)

или в скалярной форме записи

. (9)

Уравнение Беллмана представляет собой дифференциальное уравнение в частных производных. Техника определения оптимального управления их сводится к следующим процедурам

1. Из условия минимума выражения в фигурных скобках находится оптимальное управление как функция X, S, t, т.е. в форме .

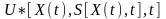2. Найденное управление подставляется в уравнение (9):

(10)

Это уравнение, содержащее только одну неизвестную функцию S(X,t), называют уравнением Гамильтона-Якоби-Беллмана.

3. Уравнение Гамильтона-Якоби решается относительно функции S[X(t),t]. При решении используется граничное условие S[X(tk),tk]=0, смысл которого очевиден из определения функции S[X(t),t]. Здесь необходимо подчеркнуть, что в настоящее время не существует универсального способа решения, позволяющего в аналитической форме найти функцию Беллмана.

4. Функцию S[X(t),t] подставляют в выражение оптимального управления , что позволяет определить его как функцию состояния и времени, т.е. в форме обратной связи .

Таким образом, если удается реализовать изложенную последовательность процедур, то метод динамического программирования позволяет в принципе решить задачу синтеза оптимальной замкнутой системы управления.

10. Техника определения оптимального управления в методе динамического программирования, достоинства и недостатки динамического программирования.

Техника определения оптимального управления их сводится к следующим процедурам

(1)

1. Из условия минимума выражения в фигурных скобках находится оптимальное управление как функция X, S, t, т.е. в форме .

2. Найденное управление подставляется в уравнение (1):

(2)

Это уравнение, содержащее только одну неизвестную функцию S(X,t), называют уравнением Гамильтона-Якоби-Беллмана.

3. Уравнение Гамильтона-Якоби решается относительно функции S[X(t),t]. При решении используется граничное условие S[X(tk),tk]=0, смысл которого очевиден из определения функции S[X(t),t]. В настоящее время не существует универсального способа решения, позволяющего в аналитической форме найти функцию Беллмана.

4. Функцию S[X(t),t] подставляют в выражение оптимального управления , что позволяет определить его как функцию состояния и времени, т.е. в форме обратной связи .

Таким образом, если удается реализовать изложенную последовательность процедур, то метод динамического программирования позволяет в принципе решить задачу синтеза оптимальной замкнутой системы управления.

Однако при применении изложенного метода необходимо иметь в виду следующее:

1. В заданном классе допустимых управлений не всегда существует такое, при котором достигается минимум в (1) ( называется допустимым, если при это управлении допустимо и функционал при нём конечен).

2. Функция Беллмана S[X,t] не всегда обладает той гладкостью, которая была использована при выводе уравнения (1).

3. Если функция S[X,t] удовлетворяет уравнению Беллмана, то отсюда не следует, что управление, при котором достигается минимум в уравнении (1), является оптимальным. В частности при этом управлении может, вообще говоря, не существовать решение уравнений движения (т.е. функционал качества будет не определён или бесконечно большим)

4. Решение уравнений Беллмана может оказаться не единственным. В этом случае требуется дополнительное исследование, позволяющее установить, какое из этих решений является функцией Беллмана исходной задачи оптимального управления.

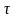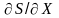Замечание. Требование непрерывной дифференцируемости функции S[X,t] является весьма ограничительным, оно не выполняется во многих задачах (например, в задачах о быстродействии при управлении двумя последовательно соединенными интеграторами. В определенной степени требуется лишь непрерывность скалярного произведения ( ) в любой момент времени t = , когда и 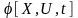разрывны.