6. Структура управления оптимального по быстродействию, определение знака управления на первом интервале.

Объект управления описывается системой (1) На управление наложены ограничения: (2). Требуется найти допустимое управление , которое за минимально возможное время Т переводит объект из заданного начального состояния в конечное состояние Х(Т)=ХТ.

Оптимизируемый функционал, в задача максимального быстродействия имеет вид (3) т.е. при оптимизации системы управления по быстродействию в интегральном функционале берется . Поэтому функция Гамильтона в этом случае (4) Так как , максимум Н реализуется одновременно с максимумом функции (5)

Согласно основной теореме принципа максимума в задаче, в которой T не фиксировано, должно выполняться условие (6)Таким образом, для оптимальности по быстродействию необходимо:

1) существование ненулевой, непрерывной векторной функции составляющие которой удовлетворяют системе (7)

2) чтобы функция при каждом значении достигала максимума по ;

3) чтобы при выполнялось соотношение (6).

Оптимальное управление определено, если известно чередование знаков управляющего воздействия на интервалах управления и значения моментов переключения . Очевидно, знак на первом интервале, определяющий в силу их чередования и знаки на всех остальных интервалах, зависит от взаимного расположения в фазовом пространстве начальной и конечной . точек фазовой траектории.

При отработке линейным объектом управления сигнала типа скачка по управляемой координате X, когда в качестве остальных фазовых координат приняты производные имеем и . В этом случае в следствии того, что на первом интервале управление должно быть таким, чтобы приблизить значение управляемой координаты к заданному, знак на первом интервале определяется знаком разности между конечным и начальным значениями управляемой координаты, т.е.

Заметим, что при ненулевых значениях других координат это правило может не действовать. Поэтому, когда необходимо определить знак первого интервала при переводе объекта из начальной точки с ненулевыми производными в заданную конечную течку, расчет производится дважды (для U=+- на первом интервале) и определяются две последовательности моментов переключения . Затем оба решения подвергают проверке на выполнения очевидного условия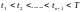 (8) Решение, которое не удовлетворяет этому условию, отбрасывают. Если оба решения удовлетворяют условию (8), то в качестве оптимального управления берут то, которое дает меньшее время управления.

7. Принцип оптимальности, понятие функции Беллмана.

Принцип оптимальности. Метод предложен американским ученым Р. Беллманом. В его основе лежит следующий простой, на первый взгляд, принцип оптимальности: оптимальное управление обладает тем свойством, что для любого начального условия и использованного начального управления последующее оптимальное управление совпадет с исходным оптимальным управлением относительно состояния, получающегося в результате применения начального управления.

Другими словами принцип оптимальности утверждает, что любой оставшийся конечный участок оптимальной траектории сам по себе так же является оптимальной траекторией.

Рассмотрим более детально это утверждение. Задача оптимального управления формулируется как задача определения управлений U*(t) и траекторией X*(t) из условия минимумов функционала

(1)

при движении объекта

(2)

из начального состояния X(t0)=X0 в конечное X(tk)=Xk под действием допустимых управляющих воздействий U(t)(U), t[t0,tk], причем время перехода tk из начального состояния в конечное не фиксировано. Здесь X(t) − n-мерный вектор состояния объекта, U(t) – m-мерный вектор управления.

Пусть поставленная задача решена и найдено оптимальное управление U*(t) и соответствующая ему оптимальная траектория X*(t). Построим эту траекторию в пространстве состояния (рис.1).

Xn

X(t0)

X*(t)

1

X*(t\)

X2

2 2\

X1 X(tk)

Рис. 1. Участки оптимальной траектории

Выделим на ней точку X*(t\), соответствующую некоторому моменту времени t0<t\<tk. Эта точка делит оптимальную траекторию на два участка − 1 и 2. Покажем, что участок 2 оптимальной траектории сам по себе является оптимальным в следующем смысле. Пусть в момент t\ объект оказался в состоянии X*(t\) и необходимо найти в области допустимых управлений такое управление и соответствующую ему траекторию, при которых для X(t\)=X*(t\). Принцип оптимальности утверждает, что такой траекторией будет участок 2 первоначальной оптимальной траектории.

Доказательство принципа просто привести методом от противного. Пусть принцип не справедлив и можно указать участок 2\, на котором интеграл меньше, чем на участке 2. Но тогда с самого начала, т.е. с момента t0 можно было бы подобрать такое управление, при котором траектория движения объекта совпала бы с кривой 1-2\. На этой траектории в силу сделанного допущения и очевидного факта

,

значение функционала I оказалось бы меньше, чем на траектории 1-2. Однако по исходным предпосылкам функционал I достигает наименьшего значения именно на траектории 1-2. Отсюда следует, что участок 2\ с указанными свойствами существовать не может и, следовательно, участок 2 является оптимальным в указанном выше смысле.

Необходимо отметить, что этот принцип оптимальности не является всеобщим – он справедлив только для систем, у которых оптимальная траектория не зависит от предыстории системы, а целиком определяется исходным ее состоянием. Например, данный принцип не справедлив для объектов с запаздываниями в его координатах.

Необходимо также подчеркнуть, что в принципе оптимальности утверждается оптимальность лишь конечного участка оптимальной траектории, а не какого либо промежуточного участка.

Предположим, что задача управления (1), (2) решена и найдено оптимальное управление U*(t) и соответствующая ему траектория движения объекта X(t). Минимальное значение критерия, соответствующее оптимальному управлению, обозначим символом:

Данная функция S(X0,t0), зависящая от начального состояния объекта X(t0)=X0 (зависимость значения критерия от конечного состояния, которое в задачах управления часто фиксировано, причем Xk=0 (задача стабилизации), не рассматривается) называется функцией Беллмана.